
【题目】已知椭圆 C 的中心在坐标原点,焦点在 X 轴上,椭圆 C 上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆 C 的标准方程;
(2)若直线 ![]() 与椭圆 C 相交于 A,B 两点( A,B 不是左右顶点),且以 AB 为直径的图过椭圆 C 的右顶点.求证:直线 l 过定点,并求出该定点的坐标.
与椭圆 C 相交于 A,B 两点( A,B 不是左右顶点),且以 AB 为直径的图过椭圆 C 的右顶点.求证:直线 l 过定点,并求出该定点的坐标.
【答案】
(1)
【解答】由题意设椭圆的标准方程为 ![]() ,由已知得:
,由已知得: ![]() ,
,![]()
所以 椭圆的标准方程为 ![]() .
.
(2)
【解答】设 ![]() .联立
.联立 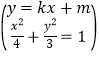
得 ![]() ,则
,则
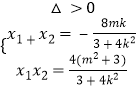
又 ![]()
因为以 AB 为直径的圆过椭圆的右顶点 ![]() ,
,
![]() ,即
,即 ![]() . 所以
. 所以![]() .
.
. .![]()
解得: ![]() ,且均满足
,且均满足 ![]() .
.
当 ![]() 时, l 的方程
时, l 的方程 ![]() ,直线过点 (2,0) ,与已知矛盾;
,直线过点 (2,0) ,与已知矛盾;
当 ![]() 时, l 的方程为
时, l 的方程为 ![]() ,直线过定点
,直线过定点 ![]() .
.
所以,直线 l 过定点,定点坐标为 ![]() .
.
【解析】(1)椭圆 ![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 ![]() 轴上,椭圆
轴上,椭圆 ![]() 上的点到焦点距离的最大值为3,最小值为1;可得
上的点到焦点距离的最大值为3,最小值为1;可得 ![]() ;进而求出椭圆的标准方程.(2)中由直线交椭圆于不同两点得不等式△>0,由中点横坐标得一方程,两者联立即可求得范围,称为“方程不等式法”,解题中注意应用.
;进而求出椭圆的标准方程.(2)中由直线交椭圆于不同两点得不等式△>0,由中点横坐标得一方程,两者联立即可求得范围,称为“方程不等式法”,解题中注意应用.


科目:高中数学 来源: 题型:
【题目】如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心, |CO| 为半径作圆,设圆C与准线l交于不同的两点M,N.
(1)若点C的纵坐标为2,求|MN| .
(2)若|AF|2=|AM|·|AN| ,求圆C的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2-a)(x-1)-2lnx(a∈R).
(1)若曲线g(x)=f(x)+x上点(1,g(1))处的切线过点(0,2),求函数g(x)的单调减区间;
(2)若函数y=f(x)在区间(0, ![]() )内无零点,求实数a的最小值.
)内无零点,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2-x+ ![]() a)的定义域为R;命题q:不等式3x-9x<a对一切正实数均成立.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围( ).
a)的定义域为R;命题q:不等式3x-9x<a对一切正实数均成立.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围( ).
A.0≤a<1
B.0≤a
C.a≤1
D.0≤a≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx(其中常数a,b∈R),g(x)=f(x)﹣f′(x)是奇函数,
(1)求f(x)的表达式;
(2)求g(x)在[1,3]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com