
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线C被直线l截得的弦长;
(Ⅱ)与直线l垂直的直线EF与曲线C相切于点Q,求点Q的直角坐标.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
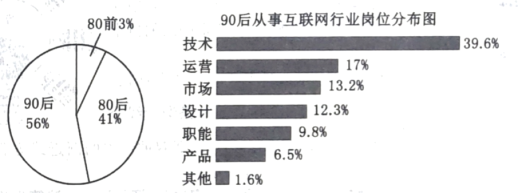
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
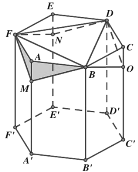
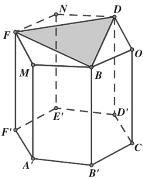
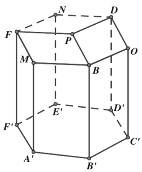
【题目】蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是![]() ,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱
,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构.如图,以下四个结论①
,就形成了蜂巢的结构.如图,以下四个结论①![]() ;②
;②![]() ;③
;③![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;④异面直线
四点共面;④异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .其中正确的个数是( ).
.其中正确的个数是( ).


A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
,![]() )的部分图象如图中实线所示,图中圆C与
)的部分图象如图中实线所示,图中圆C与![]() 的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )
的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )

A.函数![]() 的最小正周期是2π
的最小正周期是2π
B.函数![]() 的图象关于点
的图象关于点![]() 成中心对称
成中心对称
C.函数![]() 在
在![]() 单调递增
单调递增
D.将函数![]() 的图象向左平移
的图象向左平移![]() 后得到的关于y轴对称
后得到的关于y轴对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,它是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.下图为国家统计局发布的2018年2月-2019年2月全国居民消费价格指数(CPI)数据折线图(注:同比是今年第n个月与去年第n个月之比;环比表示连续2个单位周期(比如连续两月)内的量的变化比,环比增长率=(本期数-上期数)/上期数×100%).
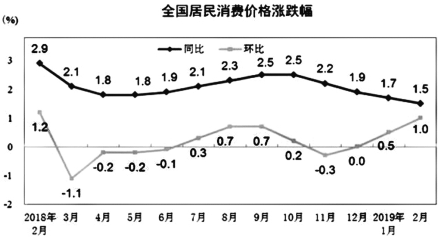
下列说法错误的是
A. 2019年2月份居民消费价格同比上涨1.5%B. 2019年2月份居民消费价格环比上涨1.0%
C. 2018年6月份居民消费价格环比下降0.1%D. 2018年11月份居民消费价格同比下降0.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用计算机生成随机数表模拟预测未来三天降雨情况,规定1,2,3表示降雨,4,5,6,7,8,9表示不降雨,根据随机生成的10组三位数:654 439 565 918 288 674 374 968 224 337,则预计未来三天仅有一天降雨的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对有![]() 个元素的总体
个元素的总体![]() 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体![]() 和
和![]() (
(![]() 是给定的正整数,且
是给定的正整数,且![]() ),再从每个子总体中各随机抽取2个元素组成样本.用
),再从每个子总体中各随机抽取2个元素组成样本.用![]() 表示元素
表示元素![]() 和
和![]() 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求![]() 的表达式(用
的表达式(用![]() ,
,![]() 表示);
表示);
(2)求所有![]() 的和.
的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com