
【题目】如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E,F分别在BC,AD上,EF∥AB,现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC. 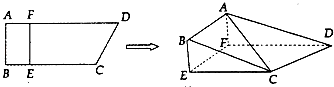
(1)若BE=3,求几何体BEC﹣AFD的体积;
(2)求三棱锥A﹣CDF的体积的最大值,并求此时二面角A﹣CD﹣E的正切值.
【答案】
(1)解:∵平面ABEF⊥平面EFDC,平面ABEF∩平面EFDC=EF,FD⊥EF,
∴FD⊥平面ABEF,又AF平面ABEF,
∴FD⊥AF,又AF⊥EF,FD∩EF=F,
∴AF⊥平面EFDC,
同理,CE⊥平面ABEF,
连结FC,将几何体BEC﹣AFD分成三棱锥A﹣CDF和四棱锥C﹣ABEF,
对于三棱锥A﹣CDF,棱锥高为AF=BE=3,FD=5,
∴V三棱锥A﹣CDF= ![]() =
= ![]() =5,
=5,
对于四棱锥C﹣ABEF,棱锥高为CE=3,
∴V四棱锥C﹣ABEF= ![]() =
= ![]() =6,
=6,
∴几何体BEC﹣AFD的体积V=V三棱锥A﹣CDF+V四棱锥C﹣ABEF=5+6=11
(2)解:设BE=x,∴AF=x(0<x≤6),FD=8﹣x,
∴V三棱锥A﹣CDF= ![]() ,
,
∴当x=4时,V三棱锥A﹣CDF有最大值,且最大值为 ![]() ,
,
在直角梯形CDEF中,EF=2,CE=2,DF=4,
∴CF=2 ![]() ,CD=2
,CD=2 ![]() ,DF=4,
,DF=4,
∴CF2+CD2=DF2,∠DCF=90°,∴DC⊥CF,
又AF⊥平面EFDC,DC平面EFDC,
∴DC⊥AF,又AF∩CF=F,∴DC⊥平面ACF,∴DC⊥AC,
∴∠ACF为二面角A﹣CD﹣E的平面角,
tan ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣CD﹣E的正切值为 ![]() .
.
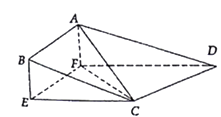
【解析】(1)推导出FD⊥平面ABEF,从而AF⊥平面EFDC,CE⊥平面ABEF,连结FC,将几何体BEC﹣AFD分成三棱锥A﹣CDF和四棱锥C﹣ABEF,由此能求出几何体BEC﹣AFD的体积.(2)设BE=x,则AF=x(0<x≤6),FD=8﹣x,V三棱锥A﹣CDF= ![]() ,当x=4时,V三棱锥A﹣CDF有最大值,∠ACF为二面角A﹣CD﹣E的平面角,由此能求出二面角A﹣CD﹣E的正切值.
,当x=4时,V三棱锥A﹣CDF有最大值,∠ACF为二面角A﹣CD﹣E的平面角,由此能求出二面角A﹣CD﹣E的正切值.


科目:高中数学 来源: 题型:
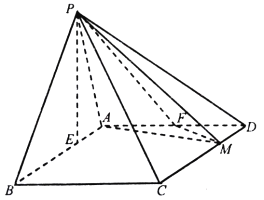
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]() 与平面
与平面![]() 所成的二面角的正弦值为
所成的二面角的正弦值为![]() 时,求四棱锥
时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图和三视图如图,M是A1B的中点,N是棱B1C1上的任意一点(含顶点). 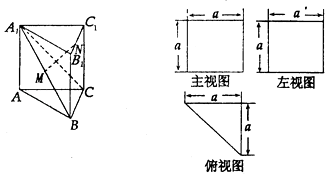
①当点N是棱B1C1的中点时,MN∥平面ACC1A1;
②MN⊥A1C;
③三棱锥N﹣A1BC的体积为VN﹣A ![]() BC=
BC= ![]() a3;
a3;
④点M是该多面体外接球的球心.
其中正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点. 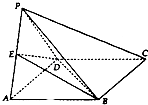
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() =1表示焦点在y轴上的椭圆;命题q:双曲线
=1表示焦点在y轴上的椭圆;命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
=1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足 ![]() =m
=m ![]() +
+ ![]() (m为常数).
(m为常数). 
(1)如图,若四边形OABP为平行四边形,求m的值;
(2)若m=2,求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 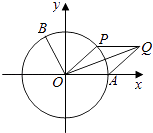
(1)求 ![]() 的值;
的值;
(2)设∠AOP=θ( ![]() ≤θ≤
≤θ≤ ![]() π),
π), ![]() =
= ![]() +
+ ![]() ,四边形OAQP的面积为S,f(θ)=(
,四边形OAQP的面积为S,f(θ)=( ![]()
![]() ﹣1)2+
﹣1)2+ ![]() S﹣1,求f(θ)的最值及此时θ的值.
S﹣1,求f(θ)的最值及此时θ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com