
【题目】在如图所示的多面体中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
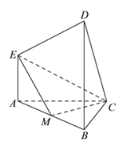
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的二面角的正弦值;
所成的二面角的正弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() . 若存在,指出点
. 若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析
(2)![]()
(3)在棱![]() 上存在一点
上存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
【解析】
(Ⅰ)由![]() ,
, ![]() 是
是![]() 的中点,得到
的中点,得到![]() ,进而得
,进而得![]() ,利用线面垂直的判定定理,证得
,利用线面垂直的判定定理,证得![]() 平面
平面![]() ,进而得到
,进而得到![]() .
.
(Ⅱ)以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴,如图建立坐标系
轴,如图建立坐标系![]() ,求得平面
,求得平面![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(Ⅲ)设![]() 且
且![]() ,求得
,求得![]() ,利用向量的夹角公式,求得
,利用向量的夹角公式,求得![]() ,即可求解.
,即可求解.
(1)证明:∵![]() ,
, ![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() .
.
(2)以![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() 为
为![]() ,
, ![]() 轴,如图建立坐标系
轴,如图建立坐标系![]() .
.
则:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,则:
,则: ![]() ,
,
取![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]()
取![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
,
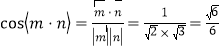 .
.
故平面![]() 与平面
与平面![]() 所成的二面角的正弦值为
所成的二面角的正弦值为![]() .
.
(3)在棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ,
,
设![]() 且
且![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
,
若直线![]() 与平面
与平面![]() 所成的的角为
所成的的角为![]() ,
,
则 ![]() ,解得
,解得![]() ,
,
所以在棱![]() 上存在一点
上存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.


科目:高中数学 来源: 题型:
【题目】直线![]() ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
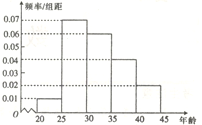
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据绘制的散点图能够看出可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明;(系数精确到0.001)
加以说明;(系数精确到0.001)
(2)建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
(系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:(1)样本![]() 的相关系数
的相关系数
(2)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 若![]() ,则“
,则“![]() ”的充分条件是“
”的充分条件是“![]() ”
”
B. 若![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
C. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
D. ![]() 是等比数列,则
是等比数列,则![]() 是
是![]() 为单调递减数列的充分条件
为单调递减数列的充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,且当x>0时,f(x)=-x2+2x+2.
(1)求f(x)的解析式;
(2)画出f(x)的图像,并指出f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在办公大厅建一面长为![]() 米的玻璃幕墙.先等距安装
米的玻璃幕墙.先等距安装![]() 根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为
根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为![]() 米的玻璃造价为
米的玻璃造价为![]() 元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为
元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为![]() 元(总造价=立柱造价+玻璃造价).
元(总造价=立柱造价+玻璃造价).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,怎样设计能使总造价最低?
时,怎样设计能使总造价最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com