
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
【答案】(Ⅰ)解: ![]() .∴
.∴ ![]() , ∵
, ∵ ![]() ,则等比数列{an}的前n项和为c﹣
,则等比数列{an}的前n项和为c﹣ ![]()
![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]()
由{an}为等比数列,得公比q= ![]()
∴ 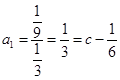 ,则c=
,则c= ![]() ,a
,a ![]()
∴ ![]()
(Ⅱ):由b1=2c=1,得s1=1
n≥2时, ![]() ,则
,则 ![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
∴ ![]() ,
, ![]() (n∈N+)
(n∈N+)
则 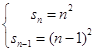 (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2).
当n=1时,b1=1满足上式
∴ ![]()
∵ ![]() =
= ![]() =
= ![]()
∴Tn= ![]() =
= ![]() =
= ![]()
由Tn= ![]() ,得n
,得n ![]() ,则最小正整数n为59
,则最小正整数n为59
【解析】(Ⅰ)由已知求得a, ![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]() ,得公比q=
,得公比q= ![]() ,即可写出通项;(Ⅱ)可得
,即可写出通项;(Ⅱ)可得 ![]() 是首项为1,公差为1的等差数列.由
是首项为1,公差为1的等差数列.由 ![]() (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2). ![]() =
= ![]() =
= ![]() ,累加求得Tn=
,累加求得Tn= ![]() ,得n
,得n ![]() ,即可得最小正整数n.
,即可得最小正整数n.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】解下列各题:
(1)求下列椭圆5x2+9y2=100的焦点和顶点的坐标;
(2)求抛物线 y2﹣6x=0的焦点坐标,准线方程和对称轴;
(3)求焦点在x轴上,两顶点间的距离是8,e= ![]() 的 双曲线的标准方程.
的 双曲线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() .过
.过![]() 三点的平面记为
三点的平面记为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(I)证明: ![]() 为
为![]() 的中点;
的中点;
(II)求此四棱柱被平面![]() 所分成上下两部分的体积之比.
所分成上下两部分的体积之比.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 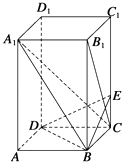
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1在平面直角坐标系中的参数方程为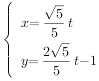 (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com