
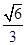 .
.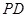 中点为
中点为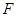 ,连接
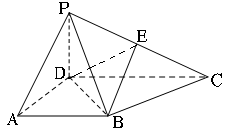
,连接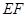 和AF;然后利用三角形的中位线的性质及空间中平行线的传递性可证BE//AF,再注意BE在平面PAD外,而AF在平面PAD内,从而可证BE∥平面PAD;(2)由已知可知直线DA、DC、DP两两互相垂直,所以我们可以
和AF;然后利用三角形的中位线的性质及空间中平行线的传递性可证BE//AF,再注意BE在平面PAD外,而AF在平面PAD内,从而可证BE∥平面PAD;(2)由已知可知直线DA、DC、DP两两互相垂直,所以我们可以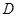 为原点,
为原点,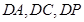 所在直线为
所在直线为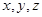 轴建立空间直角坐标系.从而由已知就可写出点P、C、A、B的坐标.进而因为E是PC的中点,求出E的坐标,然后就可写出平面BDE内不共线的两个向量的坐标,如
轴建立空间直角坐标系.从而由已知就可写出点P、C、A、B的坐标.进而因为E是PC的中点,求出E的坐标,然后就可写出平面BDE内不共线的两个向量的坐标,如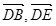 ,再设出平面BDE的一个法向量为
,再设出平面BDE的一个法向量为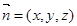 ,利用
,利用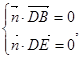 可求出平面BDE的一个法向量;而平面BDC的一个法向量显然为:
可求出平面BDE的一个法向量;而平面BDC的一个法向量显然为: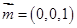 ,从而利用两法向量的夹角公式:
,从而利用两法向量的夹角公式: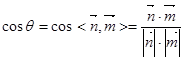 就可求得所求二面角的余弦值.
就可求得所求二面角的余弦值.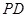 中点为
中点为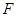 ,连接
,连接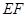 , 1分
, 1分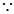 点
点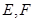 分别是
分别是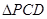 的中点,
的中点,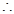
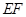
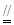
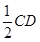 ,
,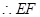
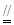
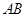 .
.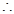 四边形
四边形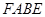 为平行四边形. 2分
为平行四边形. 2分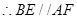 ,
,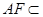 平面
平面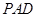 ,
, 平面
平面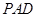 4分
4分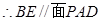 5分
5分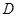 为原点,
为原点,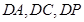 所在直线为
所在直线为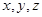 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).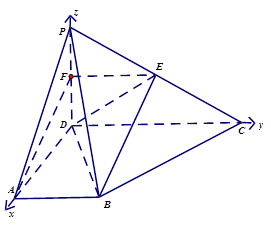
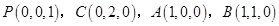 .
. 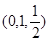 6分
6分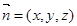 ,而
,而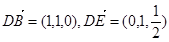
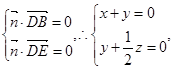 令
令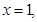 则
则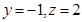 所以
所以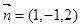 9分
9分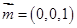
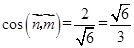 12分
12分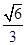 。 13分
。 13分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:填空题
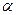 内,其余顶点在
内,其余顶点在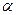 的同侧,已知其中有两个顶点到
的同侧,已知其中有两个顶点到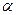 的距离分别为1和2 ,那么剩下的一个顶点到平面
的距离分别为1和2 ,那么剩下的一个顶点到平面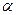 的距离可能是:①1; ②2; ③3; ④4;
的距离可能是:①1; ②2; ③3; ④4; 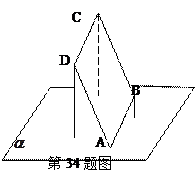
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.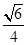 | B.-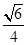 | C.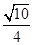 | D.-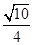 |
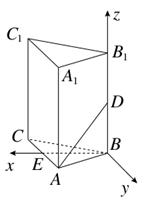
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
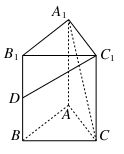
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.a,a+b,a-b | B.b,a+b,a-b |
| C.c,a+b,a-b | D.a+b,a-b,a+2b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com