
如图,设F(-c,0)是椭圆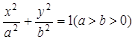 的左焦点,直线l:x=-
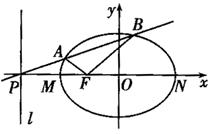
的左焦点,直线l:x=-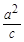 与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点P的直线m与椭圆相交于不同的两点A,B。
①证明:∠AFM=∠BFN;
②求△ABF面积的最大值。
(Ⅰ)椭圆的标准方程为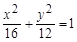 ;(Ⅱ)①详见解析;②
;(Ⅱ)①详见解析;②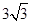 .
.
【解析】
试题分析:(Ⅰ)求椭圆的标准方程,只需利用待定系数法来求,由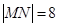 ,知
,知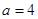 ,由
,由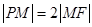 ,得
,得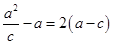 ,将
,将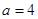 代入,可求出
代入,可求出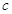 的值,从而得
的值,从而得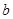 的值,由此能求出椭圆的标准方程.(Ⅱ)①证明:
的值,由此能求出椭圆的标准方程.(Ⅱ)①证明: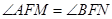 ,只需证明
,只需证明 即可,这是直线与二次曲线位置关系问题,可采用设而不求的方法,因此当
即可,这是直线与二次曲线位置关系问题,可采用设而不求的方法,因此当 的斜率为0时,
的斜率为0时,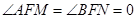 ,满足题意.当
,满足题意.当 的斜率不为0时,可设直线
的斜率不为0时,可设直线 的方程为
的方程为 ,代入椭圆方程得
,代入椭圆方程得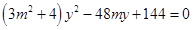 ,设出
,设出 ,有根与系数关系,及斜率公式可得
,有根与系数关系,及斜率公式可得 ,从而得到
,从而得到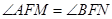 .故恒有
.故恒有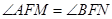 ;②求△ABF面积的最大值,由图可知
;②求△ABF面积的最大值,由图可知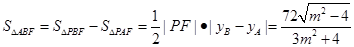 ,由基本不等式,能求出三角形ABF面积的最大值.
,由基本不等式,能求出三角形ABF面积的最大值.
试题解析:(Ⅰ)∵|MN|=8, ∴a=4, (1分)
又∵|PM|=2|MF|,∴e=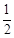 ,
(2分)
,
(2分)
∴c=2,b2=a2-c2=12,
∴椭圆的标准方程为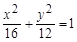 (3分)
(3分)
(Ⅱ)①证明:
当AB的斜率为0时,显然∠AFM=∠BFN=0,满足题意; (4分)
当AB的斜率不为0时,设AB的方程为x=my-8,
代入椭圆方程整理得(3m2+4)y2-48my+144=0. (5分)
△=576(m2-4), yA+yB=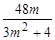 , yAyB=
, yAyB=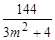 .
.
则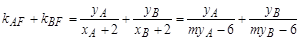
 ,
,
而2myAyB-6(yA+yB)=2m·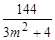 -6·
-6·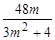 =0,
(7分)
=0,
(7分)
∴kAF+kBF=0,从而∠AFM=∠BFN.
综合可知:对于任意的割线PAB,恒有∠AFM=∠BFN. (8分)
②方法一:
S△ABF=S△PBF-S△PAF 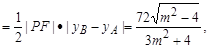 (10分)
(10分)
即S△ABF=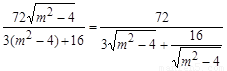
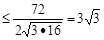 , (12分)
, (12分)
当且仅当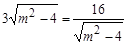 ,即m=±
,即m=±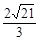 时(此时适合于△>0的条件)取到等号。
时(此时适合于△>0的条件)取到等号。
∴△ABF面积的最大值是3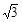 .
(13分)
.
(13分)
方法二:
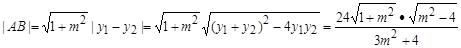
点F到直线AB的距离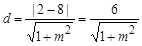 (10分)
(10分)
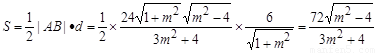
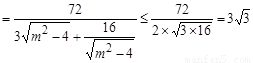 ,
(12分)
,
(12分)
当且仅当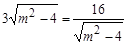 ,即m=±
,即m=±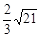 时取等号。 (13分)
时取等号。 (13分)
考点:直线与圆锥曲线的综合问题;椭圆的标准方程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△OFQ的面积为![]() ,且
,且![]() .
.
(I)设![]() ,求向量
,求向量![]() 与
与![]() 夹角
夹角![]() 的取值范围;
的取值范围;
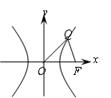
(II)若以O为中心,F为焦点的双曲线经过点Q(如图),设F(c, 0),Q(x1, y1),![]() ,当|
,当|![]() |取最小值时,求此双曲线的方程.
|取最小值时,求此双曲线的方程.
查看答案和解析>>
科目:高中数学 来源:宿松县三模 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2010年河南高三备考套数学压轴题试卷(解析版) 题型:解答题
 (a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
(a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com