
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的最小值;
的最小值;
(2)若对于任意的![]() ,都存在唯一的
,都存在唯一的![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 最小值为
最小值为![]() ,当
,当![]() 时,最小值为
时,最小值为![]() ,当
,当![]() 时,最小值为
时,最小值为![]() ;(2)
;(2)![]()
【解析】
(1)求出导函数,对a进行分类讨论求得函数的单调区间,即可求得最小值;
(2)求出![]() ,
,![]() 的值域,结合(1)的单调性和值域讨论不等关系即可得解.
的值域,结合(1)的单调性和值域讨论不等关系即可得解.
(1)由题:![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
所以函数![]() 在
在![]() 单调递增,最小值为
单调递增,最小值为![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
所以函数![]() 在
在![]() 单调递减,最小值为
单调递减,最小值为![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
所以函数的最小值为![]()
综上所述:当![]() 时,
时,![]() 最小值为
最小值为![]() ,当
,当![]() 时,最小值为
时,最小值为![]() ,当
,当![]() 时,最小值为
时,最小值为![]() ;
;
(2)函数![]() ,
,![]() ,
,![]() 当且仅当x=0时,导数值为0,
当且仅当x=0时,导数值为0,
所以![]() 在
在![]() 单调递增,值域为
单调递增,值域为![]() ,
,
结合(1)可得:
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,![]() ,只需
,只需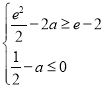 ,解得:
,解得:![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() ,不合题意,舍去,
,不合题意,舍去,
当![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
![]() ,
,![]() ,
,
所以只需![]() ,解得
,解得![]()
综上所述![]()


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆A:(x+2)2+y2=32,过B(2,0)且与圆A相切的动圆圆心为P.
(1)求点P的轨迹E的方程;
(2)设过点A的直线l1交曲线E于Q、S两点,过点B的直线l2交曲线E于R、T两点,且l1⊥l2,垂足为W(Q、S、R、T为不同的四个点),求四边形QRST的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为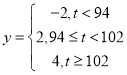 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直圆O所在的平面,
垂直圆O所在的平面,![]() 是圆O的一条直径,C为圆周上异于A,B的动点,D为弦
是圆O的一条直径,C为圆周上异于A,B的动点,D为弦![]() 的中点,
的中点,![]() .
.
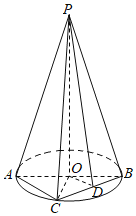
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和Sn满足2Sn=an+2﹣2,n∈N*.
(1)若数列{an}为等比数列,求数列{an}的公比q的值.
(2)若a2=a1=1,bn=an+an+1,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
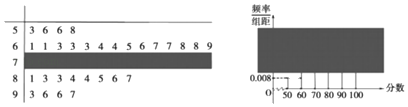
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,过A,B分别作CD的垂线,垂足分别为E,F,已知
,过A,B分别作CD的垂线,垂足分别为E,F,已知![]() ,
,![]() ,将梯形ABCD沿AE,BF同侧折起,使得平面
,将梯形ABCD沿AE,BF同侧折起,使得平面![]() 平面ABFE,平面
平面ABFE,平面![]() 平面BCF,得到图2.
平面BCF,得到图2.
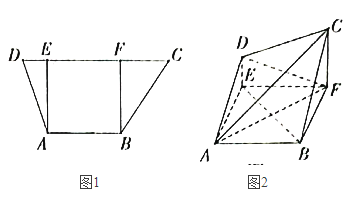
(1)证明:![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com