
分析 首先,根据函数f(x)在定义域(0,+∞)上是单调函数,若对任意x∈(0,+∞),都有f[f($\frac{1}{x}$)-x]=2,得到f($\frac{1}{x}$)-x为一个常数,以t换$\frac{1}{x}$,得f(t)-$\frac{1}{t}$=n,则f(t)-$\frac{1}{t}$=n,f(n)=2,求出n,即可求出函数的解析式,求导,即可得出结论.
解答 解:根据题意,得若对任意x∈(0,+∞),都有f[f($\frac{1}{x}$)-x]=2,得到f($\frac{1}{x}$)-x为一个常数,
以t换$\frac{1}{x}$,得f(t)-$\frac{1}{t}$=n,
则f(t)-$\frac{1}{t}$=n,f(n)=2,
∴f(t)=$\frac{1}{t}$+n,
∴f(n)=$\frac{1}{n}$+n=2,
∴n=1,
∴f(x)=1+$\frac{1}{x}$,
∴f′(x)=-$\frac{1}{{x}^{2}}$,
∴f′($\frac{1}{2}$)=-4.
故答案为:-4.
点评 本题考查的知识点是函数的值,函数解析式的求法,其中抽象函数解析式的求法,要注意对已知条件及未知条件的凑配思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 8或9 | D. | 9或10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
设数列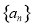 的前
的前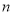 项和为
项和为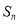 ,
,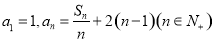 .
.
(1)证明:数列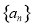 为等差数列,并分别求出
为等差数列,并分别求出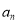 和
和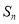 ;
;
(2)设数列 的前
的前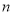 项和为
项和为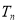 ,证明:
,证明: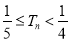 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com