
���� ��1����P��x��y������|$\overrightarrow{MN}$|•|$\overrightarrow{MP}$|+$\overrightarrow{MN}$•$\overrightarrow{NP}$=0����4$\sqrt{��x-2��^{2}+{y}^{2}}$+��-4x-8��=0���ɴ��������P�Ĺ켣C�ķ��̣�
��2����A��x1��y1����B��x2��y2������x=4-my������C�ķ��̣���y2+8my-32=0��y1+y2=-8m��y1y2=-32�������D��$\frac{{t}^{2}}{8}$��t������$\overrightarrow{DA}•\overrightarrow{DB}$=0�����ɵó����ۣ�
��� �⣺��1����P��x��y����
��M��2��0����N��-2��0����ƽ���϶���P��x��y������|$\overrightarrow{MN}$|•|$\overrightarrow{MP}$|+$\overrightarrow{MN}$•$\overrightarrow{NP}$=0��
��4$\sqrt{��x-2��^{2}+{y}^{2}}$+��-4x-8��=0��
��y2=8x��
�ද��P�Ĺ켣C�ķ���Ϊy2=8x��
��2����A��x1��y1����B��x2��y2������x=4-my������C�ķ��̣���y2=32-8my��
��y2+8my+32=0����=64m2-128��0����m��-$\sqrt{2}$��m$��\sqrt{2}$��
��y1+y2=-8m��y1y2=-32��
�����D��$\frac{{t}^{2}}{8}$��t������$\overrightarrow{DA}•\overrightarrow{DB}$=0��
�ࣨx1-$\frac{{t}^{2}}{8}$����x2-$\frac{{t}^{2}}{8}$��+��y1-t����y2-t��=0��
���������ɵ�t2-8mt+96=0��
��64m2-384��0��
��m$��-\sqrt{6}$��m$��\sqrt{6}$
��m$��-\sqrt{6}$��m$��\sqrt{6}$�����ڵ�D��ʹ�á�ABD����ABΪб�ߵ�ֱ�������Σ�
���� ���⿼��ֱ����Բ���ߵ��ۺ����⣬����Τ�ﶨ��������֪ʶ�����ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24�� | B�� | 48�� | C�� | 36�� | D�� | 28�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ɽ��C���ɽ������A������B�ĸ��Ƿֱ�Ϊ30���60�㣬��֪����ABΪ20m����ɽ��CDΪ��������
��ͼ����ɽ��C���ɽ������A������B�ĸ��Ƿֱ�Ϊ30���60�㣬��֪����ABΪ20m����ɽ��CDΪ��������| A�� | 30m | B�� | 20$\sqrt{3}$m | C�� | $\frac{40\sqrt{3}}{3}$m | D�� | 40m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
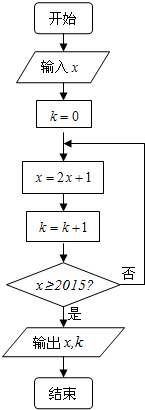
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $��\sqrt{2}$ | C�� | $\root{4}{2}$ | D�� | ��$\root{4}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD-A1B1C1D1�У�M��N�ֱ�ΪAB��B1C���е㣮
��ͼ��������ABCD-A1B1C1D1�У�M��N�ֱ�ΪAB��B1C���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com