
如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连结CD.

(1)求证:CD是⊙O的切线;
(2)过点D作DE⊥AB于点E,交AC于点P,求证:P点平分线段DE.
(1)见解析(2)见解析
【解析】(1)连结OD,
∵OC∥AD,
∴∠1=∠ADO,∠2=∠DAO.
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2.
∵OC=OC,OB=OD,
∴△DOC≌△BOC,
∴∠ODC=∠OBC.
∵OB是⊙O的半径,BC是⊙O的切线,
∴BC⊥OB,∴∠OBC=90°,
∴∠ODC=90°,∴CD⊥OD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.

(2)证法一:过点A作⊙O的切线AF,交CD的延长线于点F,则FA⊥AB.
∵DE⊥AB,由(1)知CB⊥AB,
∴FA∥DE∥CB,∴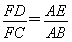 .
.
在△FAC中,∵DP∥FA,∴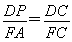 .
.
∵FA,FD是⊙O的切线,∴FA=FD,
∴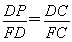 ,∴
,∴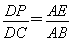
在△ABC中,∵EP∥BC,∴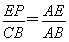 .
.
∵CD,CB是⊙O的切线,∴CB=CD,
∴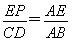 .
.
∴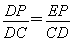 ,∴DP=EP.
,∴DP=EP.
∴点P平分线段DE.
证法二:辅助线同上.
由(1)及已知条件知BC,CD,AF为⊙O的切线,B,D,A为切点,
∴CB=CD,FA=FD.
设CD=m,FD=n.
∵DE⊥AB,∴AF∥DE∥BC.
∴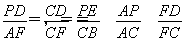 ,即PD=
,即PD=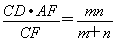 ,PE=
,PE=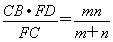 ,
,
∴PD=PE,因此P点平分线段DE.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集12讲练习卷(解析版) 题型:填空题
正四棱锥S-ABCD的底面边长为2,高为2,E是边BC的中点,动点P在棱锥表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲练习卷(解析版) 题型:解答题
设函数f(x)=|x-1|+|x-2|.
(1)画出函数y=f(x)的图象;
(2)若不等式|a+b|+|a-b|≥|a|f(x)( a≠0,a,b∈R)恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:解答题
在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为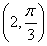 .
.
(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足3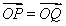 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,若直线l: 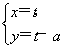 (t为参数)过椭圆C:
(t为参数)过椭圆C: (φ为参数)的右顶点,则常数a的值为________.
(φ为参数)的右顶点,则常数a的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,已知PE切⊙O于点E,割线PBA交⊙O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.
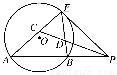
求证:(1)CE=DE;(2)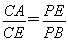 .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题抢分训练练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,O为坐标原点,A(-2,0),B(2,0),点P为动点,且直线AP与直线BP的斜率之积为- .
.
(1)求动点P的轨迹C的方程;
(2)过点D(1,0)的直线l交轨迹C于不同的两点M,N,△MON的面积是否存在最大值?若存在,求出△MON的面积的最大值及相应的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:选择题
已知a=log23.6,b=log43.2,c=log43.6,则( )
(A)a>b>c (B)a>c>b
(C)b>a>c (D)c>a>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com