
【题目】学校准备将![]() 名同学全部分配到运动会的田径、拔河和球类
名同学全部分配到运动会的田径、拔河和球类![]() 个不同项目比赛做志愿者,每个项目至少
个不同项目比赛做志愿者,每个项目至少![]() 名,则不同的分配方案有________种(用数字作答).
名,则不同的分配方案有________种(用数字作答).
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() l(a>b>0)经过点(
l(a>b>0)经过点(![]() ,1),且离心率e
,1),且离心率e![]() .
.
(1)求椭圆C的方程;
(2)若直线l与椭圆C相交于AB两点,且满足∠AOB=90°(O为坐标原点),求|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
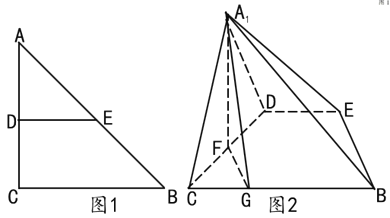
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为周期函数,证明:
为周期函数,证明:![]() 是常值函数;
是常值函数;
(3)若![]()
①记![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
②求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.
(万亿元)的折线图.

注:年份代码1~9分别对应年份2010~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2019年全国GDP的总量.
的回归方程(系数精确到0.01),预测2019年全国GDP的总量.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,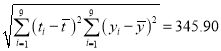 .
.
参考公式:相关系数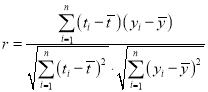 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为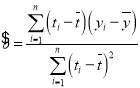 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.

(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com