练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．若将函数f（x）=x5表示为：f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，其中a0，a1，a2，…，a5为实数，则a3=10．

    分析 把f（x）=[-1+（1+x）]5 按照二项式定理展开，结合已知f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，求得a3的值．

    解答 解：f（x）=x5=[-1+（1+x）]5=-${C}_{5}^{0}$+${C}_{5}^{1}$•（1+x）-${C}_{5}^{2}$•（1+x）2+${C}_{5}^{3}$•（1+x）3-${C}_{5}^{4}$•（1+x）4+${C}_{5}^{5}$•（1+x）5，
    再根据f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，
    可得a3=${C}_{5}^{3}$=10，
    故答案为：10．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．用边长为48cm的正方形铁皮做一个无盖的铁盒时，在铁皮的四角各截去一个面积相等的小正方形，然后把四边折起，就能焊成铁盒，求小正方形边长为多少时所做的铁盒容积最大，最大值为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=x2-8lnx，g（x）=-x2+14x
    （1）若函数f（x）和函数g（x）在区间（a，a+1）上均为增函数，求实数a的取值范围；
    （2）若F（x）=$\frac{1}{4}$[g（x）-f（x）]+m-$\frac{{x}^{2}}{2}$-$\frac{7x}{2}$在[$\frac{1}{e}$，e]上有两个不同的零点，求实数m的取值范围；
    （3）试判断方程|-$\frac{1}{8}$f（x）+$\frac{1}{8}$x2-x|=$\frac{lnx}{x}$+$\frac{1}{2}$有无实数解．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．函数f（x）=ex-kx在区间（1，+∞）上单调递增，则实数k的取值范围是（-∞，e]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设一扇形的弧长为4cm，面积为4cm2，则这个扇形的圆心角的弧度数是2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

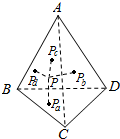    14．在平面内，可以用面积法证明下面的结论：从三角形内部任意一点，向各边引垂线，其长度分别为pa，pb，pc，且相应各边上的高分别为ha，hb，hc，则有$\frac{{p}_{a}}{{h}_{a}}+\frac{{p}_{b}}{{h}_{b}}+\frac{{p}_{c}}{{h}_{c}}$=1．
    请你运用类比的方法将此结论推广到四面体中并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设$\overrightarrow{a}$，$\overrightarrow{b}$是两个不共线的向量，已知$\overrightarrow{AB}$=2$\overrightarrow{a}$+m$\overrightarrow{b}$，$\overrightarrow{CB}$=$\overrightarrow{a}$+3$\overrightarrow{b}$，若A、B、C三点共线，则m的值为：6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．若向由f（x）=|x|+2表示的曲线与直线y=3围成的三角形内随机投掷一粒黄豆，求黄豆与点（0，2）的距离小于1的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设曲线y=x2+1在点（x，f（x））处的切线的斜率为g（x），则函数y=g（x）cosx的部分图象可以为（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案