
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且ω>0,
,且ω>0,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知 ,且函数f(x)的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求f(θ)的值;
,求f(θ)的值;
(2)求函数f(x)在[0,2π]上的单调递减区间.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】某水利部门拟在黄河沿岸修建一所水库,为大致了解甲、乙两地的降水情况,随机选取汛期月份中的一周,将这一周内每日的降水量数据进行统计(单位:![]() ),制成如图所示的茎叶图.考虑以下结论:
),制成如图所示的茎叶图.考虑以下结论:
①甲地本周的平均降水量低于乙地本周的平均降水量;
②甲地本周的中位降水量高于乙地本周的平均降水量;
③甲地本周的降水量众数大于乙地本周的降水量的中位数;
④甲地本周降水量的标准差大于乙地本周降水量的标准差.

其中根据茎叶图能得到的不恰当的统计结论的编号为( )
A.①③B.②④C.①④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《朗读者》以精美的文字,最平实的情感读出文字背后的价值,感染了众多听众,中央电视台在2018年推出了《朗读者第二季》,电视台节目组要从2018名观众中抽取50名幸运观众.先用简单随机抽样从2018人中剔除18人,剩下的2000人再按系统抽样方法抽取50人,则在2018人中,每个人被抽取的可能性 ( )
A. 都相等,且为![]() B. 都相等,且为
B. 都相等,且为![]() C. 均不相等D. 不全相等
C. 均不相等D. 不全相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然常数)时,函数
是自然常数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面中两条直线l和n相交于O,对于平面上任意一点M,若p,q分别是M到直线l和n的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.则下列说法正确的( )
A.若p=q=0,则“距离坐标”为(0,0)的点有且仅有一个
B.若pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个
C.若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个
D.若p=q,则点M的轨迹是一条过O点的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .下列命题:( )
.下列命题:( )
①函数![]() 的图象关于原点对称; ②函数
的图象关于原点对称; ②函数![]() 是周期函数;
是周期函数;
③当![]() 时,函数
时,函数![]() 取最大值;④函数
取最大值;④函数![]() 的图象与函数
的图象与函数![]() 的图象没有公共点,其中正确命题的序号是
的图象没有公共点,其中正确命题的序号是
(A)①③ (B)②③ (C)①④ (D)②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,E,F分别为A1C1和BC的中点,M,N分别为A1B和A1C的中点.求证:
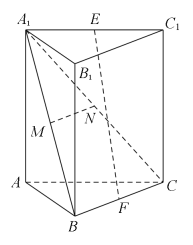
(1)MN∥平面ABC;
(2)EF∥平面AA1B1B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com