
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.
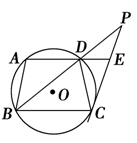
(1)求证:AB2=DE·BC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:填空题
设圆x2+y2=2的切线l与x轴正半轴、y轴正半轴分别交于点A,B,当|AB|取最小值时,切线l的方程为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:选择题
公比为2的等比数列{an}的各项都是正数,且a3a11=16,则a5=( ).
A.1 B.2 C.4 D.8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
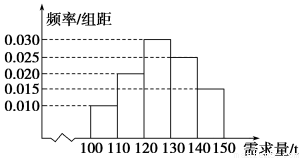
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
记△ABC各边的中点分别为D,E,F,在A,B,C,D,E,F中任取4点,若这4点为平行四边形顶点,则称为选取成功.某人连续进行3次这种选取,则至少成功1次的概率是( ).
A.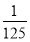 B.
B.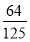 C.
C.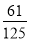 D.
D.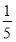
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,点D在⊙O的弦AB上移动,AB=4,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,⊙O的割线PBA过圆心O,弦CD交PA于点F,且△COF∽△PDF,若PB=OA=2,则PF=________.
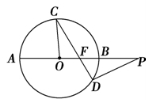
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:选择题
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ=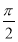 ”的( ).
”的( ).
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:选择题
若函数y=f(x)(x∈R)满足f(x+1)=-f(x),且x∈[-1,1]时f(x)=1-x2.函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
A.7 B.8?,
C.9 D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com