
分析 (1)利用任意角的三角函数的定义,求得sinα和cosα的值.
(2)由条件利用诱导公式进行化简所给的式子,可得结果.
解答 解:(1)∵角α的终边经过点P(-3,4),∴x=-3,y=4,r=5,
∴$sinα=\frac{y}{r}=\frac{4}{5},cosα=\frac{x}{r}=-\frac{3}{5}$.
(2)$\frac{{sin(2π-α)cos(π+α)cos(\frac{π}{2}+α)cos(\frac{11π}{2}-α)}}{{cos(π-α)sin(3π-α)sin(-π-α)sin(\frac{9π}{2}+α)}}$=$\frac{(-sinα)(-cosα)(-sinα)(-sinα)}{(-cosα)sinαsinαcosα}$=$-tanα=\frac{-sinα}{cosα}=-\frac{4}{3}$.
点评 本题主要考查任意角的三角函数的定义,利用诱导公式进行化简求值,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 30° | D. | 0° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (-1,0)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)≤bf(a) | B. | bf(a)≤af(b) | C. | af(a)≤f(b) | D. | bf(b)≤f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
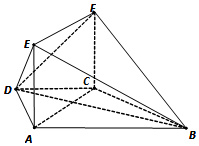 在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.
在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com