
【题目】《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为![]() ,且每加工处理一吨厨余垃圾得到的产品售价为16元.
,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(Ⅰ)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(Ⅱ)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则需要市政府至少补贴多少元才能使该企业不亏损?
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于-1的直线与椭圆
且斜率等于-1的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
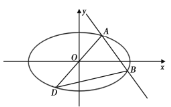
(1)证明:直线![]() 的斜率为定值;
的斜率为定值;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 在回归模型中,预报变量![]() 的值不能由解释变量
的值不能由解释变量![]() 唯一确定
唯一确定
B. 若变量![]() ,
,![]() 满足关系
满足关系![]() ,且变量
,且变量![]() 与
与![]() 正相关,则
正相关,则![]() 与
与![]() 也正相关
也正相关
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高速公路隧道设计为单向三车道,每条车道宽4米,要求通行车辆限高5米,隧道全长1.5千米,隧道的断面轮廓线近似地看成半个椭圆形状(如图所示).

(1)若最大拱高![]() 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽![]() 至少是多少米?(结果取整数)
至少是多少米?(结果取整数)
(2)如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
参考数据:![]() ,椭圆的面积公式为
,椭圆的面积公式为![]() ,其中
,其中![]() ,
,![]() 分别为椭圆的长半轴和短半轴长.
分别为椭圆的长半轴和短半轴长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
(1)在频率分布直方图中,中位数左边和右边的直方图的面积相等.
(2)如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变.
(3)一个样本的方差s2=![]() [(x
[(x![]() 一3)2+(X
一3)2+(X![]() —3)2+ +(X
—3)2+ +(X![]() 一3)2],则这组数据总和等于60.
一3)2],则这组数据总和等于60.
(4)数据![]() 的方差为
的方差为![]() ,则数据
,则数据![]() 的方差为
的方差为![]() .
.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友某日在某淘宝店的网购情况,随机抽查了该市当天![]() 名网友的网购金额情况,得到如下统计表(如图).
名网友的网购金额情况,得到如下统计表(如图).
网购金额(单位:千元) | 频数 | 频率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若网购金额超过![]() 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过![]() 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为![]() .
.
(Ⅰ)试确定![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(Ⅱ)该营销部门为了进一步了解这![]() 名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取
名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取![]() 人,若需从这
人,若需从这![]() 人中随机选取
人中随机选取![]() 人进行问卷调查.设
人进行问卷调查.设![]() 为选取的
为选取的![]() 人中“网购达人”的人数,求
人中“网购达人”的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
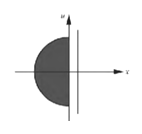
【题目】关于旋转体的体积,有如下的古尔丁(guldin)定理:“平面上一区域D绕区域外一直线(区域D的每个点在直线的同侧,含直线上)旋转一周所得的旋转体的体积,等于D的面积与D的几何中心(也称为重心)所经过的路程的乘积”.利用这一定理,可求得半圆盘 ,绕直线x
,绕直线x![]() 旋转一周所形成的空间图形的体积为_____.
旋转一周所形成的空间图形的体积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机器生产商,对一次性购买两台机器的客户推出两种超过质保期后两年内的延保维修方案:
方案一:交纳延保金![]() 元,在延保的两年内可免费维修
元,在延保的两年内可免费维修![]() 次,超过
次,超过![]() 次每次收取维修费
次每次收取维修费![]() 元;
元;
方案二:交纳延保金![]() 元,在延保的两年内可免费维修
元,在延保的两年内可免费维修![]() 次,超过
次,超过![]() 次每次收取维修费
次每次收取维修费![]() 元.
元.
某工厂准备一次性购买两台这种机器,现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了台这种机器超过质保期后延保两年内维修的次数,统计得下表:
维修次数 | 0 | 1 | 2 | 3 |
机器台数 | 20 | 10 | 40 | 30 |
以上![]() 台机器维修次数的频率代替一台机器维修次数发生的概率,记
台机器维修次数的频率代替一台机器维修次数发生的概率,记![]() 表示这两台机器超过质保期后延保两年内共需维修的次数.
表示这两台机器超过质保期后延保两年内共需维修的次数.
![]() 求
求![]() 的分布列;
的分布列;
![]() 以所需延保金与维修费用之和的期望值为决策依据,该工厂选择哪种延保方案更合算?
以所需延保金与维修费用之和的期望值为决策依据,该工厂选择哪种延保方案更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com