
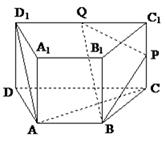

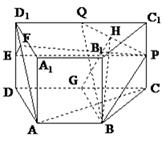
 又D1Q=AB=1,D1Q∥AB,
又D1Q=AB=1,D1Q∥AB,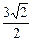 ,PE="2 " ∴EF=
,PE="2 " ∴EF=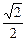 又D1E=
又D1E=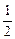 ,D1D=1,∴AD="1 "
,D1D=1,∴AD="1 " 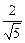 ,又BG=1,得tan∠BHG=
,又BG=1,得tan∠BHG=



科目:高中数学 来源:不详 题型:解答题
 是
是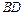 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角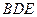 ?若存在,确定点N的位置;
?若存在,确定点N的位置;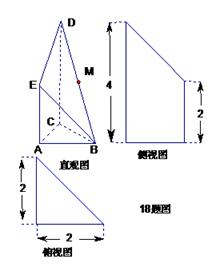
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
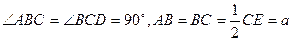 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在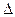 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以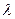 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0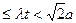 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
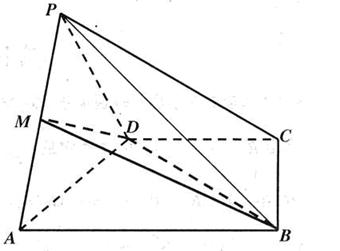
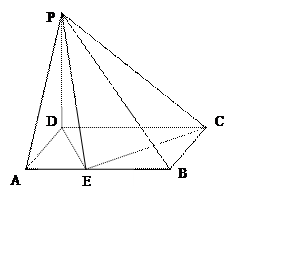 已知PD=
已知PD=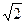 ,CD=2,AE=
,CD=2,AE=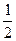 ,
,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
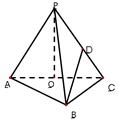
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com