
【题目】珠海市某学校的研究性学习小组,对昼夜温差(最高温度与最低温度的差)大小与绿豆种子一天内出芽数之间的关系进行了研究,该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的![]() 颗绿豆种子当天内的出芽数(如图2)
颗绿豆种子当天内的出芽数(如图2)
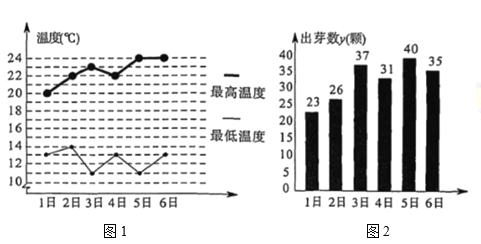
已知绿豆种子出芽数![]() (颗) 和温差
(颗) 和温差![]() 具有线性相关关系.
具有线性相关关系.
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() 的回归方程
的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为![]() ,估计4月7日浸泡的
,估计4月7日浸泡的![]() 颗绿豆种子一天内的出芽数.
颗绿豆种子一天内的出芽数.
附: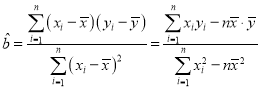 ,
,![]() .
.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,己知圆
中,己知圆![]() ,且圆
,且圆![]() 被直线
被直线![]() 截得的弦长为2.
截得的弦长为2.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 的切线
的切线![]() 在
在![]() 轴和
轴和![]() 轴上的截距相等,求切线
轴上的截距相等,求切线![]() 的方程;
的方程;
(3)若圆![]() 上存在点
上存在点![]() ,由点
,由点![]() 向圆
向圆![]() 引一条切线,切点为
引一条切线,切点为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,椭圆的右焦点
上,椭圆的右焦点![]() ,直线
,直线![]() 过椭圆的右顶点
过椭圆的右顶点![]() ,与椭圆交于另一点
,与椭圆交于另一点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为弦
为弦![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点的坐标,若不存在,请说明理由;
点的坐标,若不存在,请说明理由;
(3)若![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,求
,求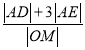 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛A的正南B处,以![]() 的速度向正北航行,
的速度向正北航行,![]() ,同时乙船自岛A出发以
,同时乙船自岛A出发以![]() 的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间为( )
的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ADC=60°,AD=AC=2,O为AC的中点,PO⊥平面ABCD且PO=4,M为PD的中点.
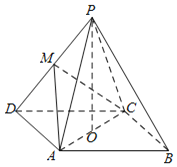
(1)证明:MO∥平面PAB;
(2)求直线AM与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有编号为![]() 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:
编号 |
|
|
|
|
|
|
|
|
|
|
直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.51 | 1.47 | 1.46 | 1.53 | 1.47 |
其中直径在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)上述10个零件中,随机抽取1个,求这个零件为一等品的概率.
(2)从一等品零件中,随机抽取2个;
①用零件的编号列出所有可能的抽取结果;
②求这2个零件直径相等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com