分析:(1)连接D
1B、BC
1,则易得EF∥D
1B故要证EF⊥B
1C只需证D
1B⊥B
1C则根据正方体ABCD-A
1B
1C
1D
1中的性质易得D
1B在平面BC
1上的射影为BC
1且BC
1⊥B
1C故根据三垂线定理即可得证.
(2)根据图形分析可知所求的二面角F-EG-C
1的大小为钝角故可先求求其补角即二面角F-EG-D的大小.则根据正方体的性质可得取DC的中点M,连接FM,则FM⊥DC.过M做MN⊥EG于N点,连接FN,由三垂线定理可证FN⊥EG故∠MNF的邻补角为二面角F-EG-C
1的平面角.然后结合题中的条件在Rt△FMN中,∠MNF=90°中即可求出∠MNF的三角函数值则二面角F-EG-C
1的平面角即为此角的补角.
另外此题也可用空间向量来求解.可建立如图所示的空间直角坐标系且令AB=4
(1)可求出
=(2,2,-2),
=(-4,0,-4)再利用向量数量积的坐标计算可得
•=0即可证得EF⊥B
1C.
(2)求出平面FEG的法向量为
平面C
1EG的法向量
然后利用向量的夹角公式求出cos
<,>.如果cos
<,>>0则所求的二面角F-EG-C
1的大小为π-
<,>如果cos
<,><0则则所求的二面角F-EG-C
1的大小为
<,>.
解答:解:
解法一:
(Ⅰ)连接D
1B、BC
1
∵E、F是D
1D、BD的中点,
∴EF∥D
1B,且EF=
D1B又∵D
1C
1⊥平面BC
1∴D
1B在平面BC
1上的射影为BC
1.
∵BC
1⊥B
1C
∴由三垂线定理知B
1C⊥D
1B
∴EF⊥B
1C
(Ⅱ)取DC的中点M,连接FM,则FM⊥DC.过M做MN⊥EG于N点,连接FN
∴由三垂线定理可证FN⊥EG
∴∠MNF的邻补角为二面角F-EG-C
1的平

面角
设正方体的棱长为4,则FM=2
在Rt△EDG中,△EDG~△MNG,
∴
MN===.
在Rt△FMN中,∠MNF=90°
∴tan∠MNF=
=∴∠MNF=arctan
∴二面角F-EG-C
1的大小为
π-arctan解法2:建立如图直角坐标系,令AB=4,则D(0,0,0),A(4,0,0),B(4,4,0),C(0,4,0),D
1(0,0,4),C
1(0,4,4),E(0,0,2),F(2,2,0),G(0,3,0),B
1(4,4,4).
(1)∵
=(2,2,-2),
=(-4,0,-4)∵
•=0∴EF⊥B1C(3)设平面FEG的法向量为
=(x1,y1,z1),平面C
1EG的法向量
=(1,0,0)=(2,2,-2)=(0,3,-2)∵
•=2x1+2y1-2z1=0•=3y1-2z1=0∴
=(1,2,3)cosθ===故二面角F-EG-C
1的大小为
π-arccos 点评:本题主要考察了线线垂直的证明和二面角的求解.解题的关键是关于线线垂直的证明可利用三垂线定理证(如法一)也可以利用空间向量来证(如法二)而对于二面角的求解可采用定义法即找到一个面到另一个面的一条垂线然后再利用三垂线定理即可作出二面角的平面角,另外也可利用空间向量求解二面角即求出二面角的两个半平面的法向量然后利用向量的夹角公式求出法向量的夹角的余弦值再结合图形特征和法向量的夹角的余弦值的正负得出二面角的大小是法向量的夹角还是其补角!

 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG= 面角
面角

 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=![]() CD。
CD。

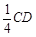 .
. 