
【题目】已知奇函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)判断函数![]() 的单调性,并给出证明;
的单调性,并给出证明;
(3)若函数![]() 在区间
在区间![]() 上有两个不同的零点,求m的取值范围.
上有两个不同的零点,求m的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)根据当![]() 有意义的奇函数图象过坐标原点,
有意义的奇函数图象过坐标原点,![]() ,求得参数的值,利用不等式的性质求函数的值域,得到结果;
,求得参数的值,利用不等式的性质求函数的值域,得到结果;
(2)应用定义判断并证明函数的单调性;
(3)利用函数零点的个数,对式子进行化简,转化为对应方程有两个不等实根,考虑函数图象的走向,求得结果.
(1)因为函数![]() 为奇函数,且定义域为R,
为奇函数,且定义域为R,
所以有![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以函数![]() 的值域为
的值域为![]() ;
;
(2)![]() 为
为![]() 上的增函数,证明如下:
上的增函数,证明如下:
任取![]() ,且
,且![]() ,则
,则
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以函数![]() 为
为![]() 上的增函数;
上的增函数;
(3)函数![]() 在区间
在区间![]() 上有两个不同的零点,
上有两个不同的零点,
即![]() 在
在![]() 上有两个不同的实数根,
上有两个不同的实数根,
整理得![]() ,
,
设![]() ,所以
,所以![]() ,
,
则当![]() 时,
时,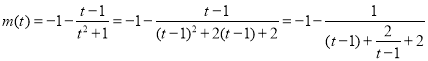 ,
,
综合考虑可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
且![]() ,
,![]() ,
,![]() ,
,
要使函数有两个零点,可以得到![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-a|.
(1)当a=2时,解不等式f(x)≥4-|x-1|;
(2)若f(x)≤1的解集为[0,2],![]() (m>0,n>0),求证:m+2n≥4.
(m>0,n>0),求证:m+2n≥4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
,![]() ,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若
,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若![]() 平面ABC,则三棱锥
平面ABC,则三棱锥![]() 的四个面都是直角三角形;②若
的四个面都是直角三角形;②若![]() 平面ABC,且M是边AB的中点,则有
平面ABC,且M是边AB的中点,则有![]() ;③若
;③若![]() ,
,![]() 平面ABC,则
平面ABC,则![]() 面积的最小值为
面积的最小值为![]() ;④若
;④若![]() ,P在平面ABC上的射影是
,P在平面ABC上的射影是![]() 内切圆的圆心,则点P到平面ABC的距离为
内切圆的圆心,则点P到平面ABC的距离为![]() .其中正确命题的序号是________.(把你认为正确命题的序号都填上)
.其中正确命题的序号是________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的数学家刘徽著有《海岛算经》.内有一篇:“今有望海岛,立两表齐、高三丈,前后相去千步,今后表与前表相直,从前表却行百二十三步,人目著地望岛峰,与表末参合.从后表却行百二十七步,人目著地取望岛峰,亦与表末参合.问岛高及去表各几何?”(参考译文:假设测量海岛,立两根标杆,高均为5步,前后相距1000步,令前后两根标杆的底部和岛的底部在同一水平直线上,从前标杆退行123步,人的视线从地面(人的高度忽略不计)过标杆顶恰好观测到岛峰,从后标杆退行127步,人的视线从地面过标杆顶恰好观测到岛峰,问岛高多少?岛与前标杆相距多远?)(丈、步为古时计量单位,三丈=5步).则海岛高度为
A. 1055步 B. 1255步 C. 1550步 D. 2255步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市工业部门计划对所辖中小型企业推行节能降耗技术改造,下面是对所辖企业是否支持技术改造进行的问卷调查的结果:
支持 | 不支持 | 合计 | |
中型企业 | 40 | ||
小型企业 | 240 | ||
合计 | 560 |
已知从这560家企业中随机抽取1家,抽到支持技术改造的企业的概率为![]() .
.
(1)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(2)从上述支持节能降耗的中小企业中按分层抽样的方法抽出12家企业,然后从这12家企业选出9家进行奖励,分别奖励中型企业50万元,小型企业10万元.设![]() 为所发奖励的金额.
为所发奖励的金额.
求![]() 的分布列和期望.
的分布列和期望.
附:![]()
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数),其中
为自然对数的底数),其中![]() .
.
(1)在区间![]() 上,
上,![]() 是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(2)若函数![]() 的两个极值点为
的两个极值点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为F,已知直线
的焦点为F,已知直线![]() 与抛物线C交于A,B两点(A,B两点分别在
与抛物线C交于A,B两点(A,B两点分别在![]() 轴的上、下方).
轴的上、下方).
(1)求证:![]() ;
;
(2)已知弦长![]() ,试求:过A,B两点,且与直线
,试求:过A,B两点,且与直线![]() 相切的圆D的方程.
相切的圆D的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com