
【题目】设n为正整数,集合A=![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .对于集合A中的任意元素
.对于集合A中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(Ⅰ)当n=3时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)当![]() 时,对于
时,对于![]() 中的任意两个不同的元素
中的任意两个不同的元素![]() ,
,![]() ,证明:
,证明:![]() .
.
(Ⅲ)给定不小于2的正整数n,设B是A的子集,且满足:对于B中的任意两个不同元素![]() ,
,![]() ,
,![]() .写出一个集合B,使其元素个数最多,并说明由.
.写出一个集合B,使其元素个数最多,并说明由.
【答案】(Ⅰ)2,2;(Ⅱ)证明见解析;(Ⅲ)见解析.
【解析】
(Ⅰ)根据定义直接计算即可;
(Ⅱ)设![]() ,
,![]() ,有
,有![]() ,
,![]() ,可得
,可得![]() ,
,
所以![]() ,易得
,易得![]() ,
, ![]()
![]()
![]() ,即可证明结论.
,即可证明结论.
(Ⅲ)根据抽屉原理即可得证.
(Ⅰ)因为![]() ,
,![]() ,
,
所以![]() ,
,
![]() ;
;
(Ⅱ)当![]() 时,对于
时,对于![]() 中的任意两个不同的元素
中的任意两个不同的元素![]() ,
,
设![]() ,
,![]() ,有
,有
![]() ,
,![]() .
.
对于任意的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,有
时,有![]() ,
,
当![]() 时,有
时,有![]() .
.
即![]() ,
,
所以,有![]() ,
,
又因为![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
所以,![]()
![]()
![]() ,
,
即![]() ,当且仅当
,当且仅当![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )时等号成立;
)时等号成立;
(Ⅲ)由(Ⅱ)可证,对于任意的![]() ,
,
若![]() ,则
,则![]() ,
,![]() 成立.
成立.
所以,考虑设
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
对于任意的![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
假设满足条件的集合B中元素个数不少于![]() ,
,
则至少存在两个元素在某个集合![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )中,
)中,
不妨设为![]() ,则
,则![]() .
.
与假设矛盾,所以满足条件的集合B中元素个数不多于![]() .
.
取![]() ;
;
对于![]() ,
,![]() ,
,![]() ,
,![]() ,取
,取![]() ,且
,且![]() ;
;![]() .
.
令![]() ,
,
则集合![]() 满足条件,且元素个数为
满足条件,且元素个数为![]() ,
,
故![]() 是一个满足条件且元素个数最多的集合.
是一个满足条件且元素个数最多的集合.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .点E为椭圆在第一象限内一点,点F在椭圆上且与点E关于原点对称,直线
.点E为椭圆在第一象限内一点,点F在椭圆上且与点E关于原点对称,直线![]() 与椭圆交于A,B两点,则点E,F到直线x+y-1=0的距离之和的最大值是________;此时四边形AEBF的面积是________.
与椭圆交于A,B两点,则点E,F到直线x+y-1=0的距离之和的最大值是________;此时四边形AEBF的面积是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网上购物的普及,传统的实体店遭受到了强烈的冲击,某商场实体店近九年来的纯利润如下表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
实体店纯利润 | 2 | 2.3 | 2.5 | 2.9 | 3 | 2.5 | 2.1 | 1.7 | 1.2 |
根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.254;根据后5年的数据,对
作线性相关性检验,求得样本相关系数的绝对值为0.254;根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.985;
作线性相关性检验,求得样本相关系数的绝对值为0.985;
(1)如果要用线性回归方程预测该商场2019年实体店纯利润,现有两个方案:
方案一:选取这9年的数据,进行预测;
方案二:选取后5年的数据进行预测.
从生活实际背景以及相关性检验的角度分析,你觉得哪个方案更合适.
附:相关性检验的临界值表:
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
(2)某机构调研了大量已经开店的店主,据统计,只开网店的占调查总人数的![]() ,既开网店又开实体店的占调查总人数的
,既开网店又开实体店的占调查总人数的![]() ,现以此调查统计结果作为概率,若从上述统计的店主中随机抽查了5位,求只开实体店的人数的分布列及期望.
,现以此调查统计结果作为概率,若从上述统计的店主中随机抽查了5位,求只开实体店的人数的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下(提示:可以用第(2)问的结论),对任意的![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家正积极推行垃圾分类工作,教育部办公厅等六部门也发布了《关于在学校推进生活垃圾分类管理工作的通知》.《通知》指出,到2020年底,各学校生活垃圾分类知识普及率要达到100%某市教育主管部门据此做了“哪些活动最能促进学生进行垃圾分类”的问卷调查(每个受访者只能在问卷的4个活动中选择一个)如图是调查结果的统计图,以下结论正确的是( )
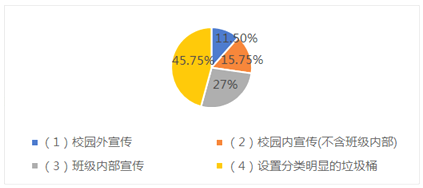
A.回答该问卷的受访者中,选择的(2)和(3)人数总和比选择(4)的人数多
B.回该问卷的受访者中,选择“校园外宣传”的人数不是最少的
C.回答该问卷的受访者中,选择(4)的人数比选择(2)的人数可能多30人
D.回答该问卷的总人数不可能是1000人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com