
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD是矩形,平面DCC1D1⊥平面ABCD.AD=3,CD=DD1=5,∠D1DC=120°,M,N分别是线段AD1,BD的中点.

(1)求证:MN//平面DCC1D1;
(2)求证:MN⊥平面ADC1;
(3)求三棱锥D1﹣ADC1的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
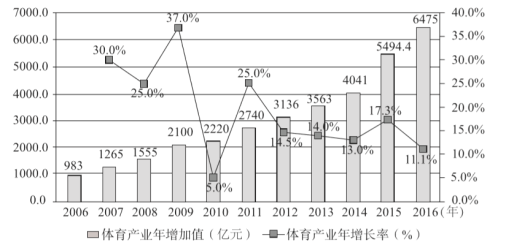
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4,5这六个数字组成无重复数字的四位数.
(1)在组成的四位数中,求所有偶数的个数;
(2)在组成的四位数中,求比2430大的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均为正数的等差数列.
是各项均为正数的等差数列.
(1)若![]() ,且
,且![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)在(1)的条件下,数列![]() 的前
的前![]() 和为
和为![]() ,设
,设![]() ,若对任意的
,若对任意的![]() ,不等式
,不等式![]() 恒成立,求突数
恒成立,求突数![]() 的最小值:
的最小值:
(3)若数列![]() 中有两项可以表示位某个整数
中有两项可以表示位某个整数![]() 的不同次冪,求证:数列
的不同次冪,求证:数列![]() 中存在无穷多项构成等比数列.
中存在无穷多项构成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率
)的离心率![]() ,直线
,直线![]() 被以椭圆
被以椭圆![]() 的短轴为直径的圆截得的弦长为
的短轴为直径的圆截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两个不同的点,且
两个不同的点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币向上抛掷三次,下列两个事件中,是对立事件的是( )
A.事件![]() :“恰有两次正面向上”,事件
:“恰有两次正面向上”,事件![]() :“恰有两次反面向上”
:“恰有两次反面向上”
B.事件![]() :“恰有两次正面向上”,事件
:“恰有两次正面向上”,事件![]() :“恰有一次正面向上”
:“恰有一次正面向上”
C.事件![]() :“至少有一次正面向上”,事件
:“至少有一次正面向上”,事件![]() :“至多一次正面向上”
:“至多一次正面向上”
D.事件![]() :“至少有一次正面向上”,事件
:“至少有一次正面向上”,事件![]() :“恰有三次反面向上”
:“恰有三次反面向上”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com