
【题目】交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 | A1 | A2 | A3 | A4 | A5 | A6 |
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
【答案】解:(Ⅰ)由题意可知X的可能取值为0.9a,0.8a,0.7a,a,1.1a,1.3a. 由统计数据可知:
P(X=0.9a)= ![]() ,P(X=0.8a)=
,P(X=0.8a)= ![]() ,P(X=0.7a)=
,P(X=0.7a)= ![]() ,P(X=a)=
,P(X=a)= ![]() ,P(X=1.1a)=
,P(X=1.1a)= ![]() ,
,
P(X=1.3a)= ![]() .
.
所以X的分布列为:
X | 0.9a | 0.8a | 0.7a | a | 1.1a | 1.3a |
P |
|
|
|
|
|
|
所以EX=0.9a× ![]() +0.8a×
+0.8a× ![]() +0.7a×
+0.7a× ![]() +a×
+a× ![]() +1.1a×
+1.1a× ![]() +1.3a×
+1.3a× ![]() =
= ![]() =
= ![]() ≈942.
≈942.
(Ⅱ) ①由统计数据可知任意一辆该品牌车龄已满三年的二手车为事故车的概率为 ![]() ,三辆车中至多有一辆事故车的概率为P=
,三辆车中至多有一辆事故车的概率为P= ![]() +
+ ![]() =
= ![]() .
.
②设Y为该销售商购进并销售一辆二手车的利润,Y的可能取值为﹣5000,10000.
所以Y的分布列为:
Y | ﹣5000 | 10000 |
P |
|
|
所以EY=﹣5000× ![]() +10000×
+10000× ![]() =5000.
=5000.
所以该销售商一次购进100辆该品牌车龄已满三年的二手车获得利润的期望值为100EY=50万元
【解析】(Ⅰ)由题意可知X的可能取值为0.9a,0.8a,0.7a,a,1.1a,1.3a.由统计数据可知其概率及其分布列.(II)①由统计数据可知任意一辆该品牌车龄已满三年的二手车为事故车的概率为 ![]() ,三辆车中至多有一辆事故车的概率为P=
,三辆车中至多有一辆事故车的概率为P= ![]() +
+ ![]() . ②设Y为该销售商购进并销售一辆二手车的利润,Y的可能取值为﹣5000,10000.即可得出分布列与数学期望.
. ②设Y为该销售商购进并销售一辆二手车的利润,Y的可能取值为﹣5000,10000.即可得出分布列与数学期望.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
(I)若直线l1的倾斜角为 ![]() ,求△ABM的面积S的值;
,求△ABM的面积S的值;
(Ⅱ)过点B作直线BN⊥l于点N,证明:A,M,N三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),则y1 , y2 , …y2017的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣DEF中,侧面ABED是边长为2的菱形,且∠ABE= ![]() ,BC=
,BC= ![]() ,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=
,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM= ![]() CF.
CF.
(Ⅰ)证明:直线GM∥平面DEF;
(Ⅱ)求二面角M﹣AB﹣F的余弦值.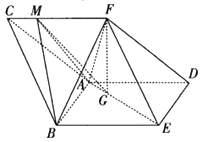
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ﹣
(a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ﹣ ![]() )=
)= ![]() .
.
(Ⅰ)若曲线C与l只有一个公共点,求a的值;
(Ⅱ)A,B为曲线C上的两点,且∠AOB= ![]() ,求△OAB的面积最大值.
,求△OAB的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,若椭圆与圆
,若椭圆与圆![]() :
:![]() 相交于M,N两点,且圆E在椭圆内的弧长为
相交于M,N两点,且圆E在椭圆内的弧长为![]() .
.
(1)求椭圆的方程;
(2)过椭圆的上焦点作两条相互垂直的直线,分别交椭圆于A,B、C,D,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某河流在一段时间x min内流过的水量为y m3,y是x的函数,y=f(x)=![]() .
.
(1)当x从1变到8时,y关于x的平均变化率是多少?它代表什么实际意义?
(2)求f′(27)并解释它的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个焦点与抛物线
(a>b>0)的一个焦点与抛物线 ![]() 的焦点相同,F1 , F2为椭圆的左、右焦点.M为椭圆上任意一点,△MF1F2面积的最大值为4
的焦点相同,F1 , F2为椭圆的左、右焦点.M为椭圆上任意一点,△MF1F2面积的最大值为4 ![]() .
.
(1)求椭圆C的方程;
(2)设椭圆C上的任意一点N(x0 , y0),从原点O向圆N:(x﹣x0)2+(y﹣y0)2=3作两条切线,分别交椭圆于A,B两点.试探究|OA|2+|OB|2是否为定值,若是,求出其值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com