
本题满分10分)
设函数
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。
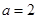 ,
,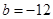 ,
,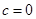 .
.
【解析】
试题分析:由y=f(x)为奇函数,知c=0,故f(x)=ax3+bx,所以f'(x)=3ax2+b,f'(1)=3a+b=-6,由导数f'(x)的 最小值为-12,知b=-12,由此能求出a,b,c的值.
解:∵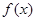 为奇函数,∴
为奇函数,∴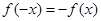
即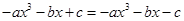 ∴
∴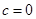 (4分)
(4分)
∵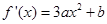 的最小值为
的最小值为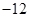 ∴
∴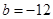 (6分)
(6分)
又直线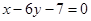 的斜率为
的斜率为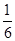 因此,
因此, (8分)
(8分)
∴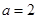 ,
,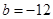 ,
,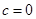 .(10分)
.(10分)
考点:本题主要考查了导数的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
点评:解决该试题的关键是理解导数几何意义的运用明确导数的值即为该点处的切线的斜率,只要只要点的坐标和导数值,既可以写出切线方程。


科目:高中数学 来源:2012届浙江省台州中学高三上学期第一次统练理科数学 题型:解答题
(本题满分10分)设函数 ,
,
(1)若函数 在
在 处与直线
处与直线 相切;
相切;
①求实数 的值;②求函数
的值;②求函数 上的最大值;
上的最大值;
(2)当 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(二)文数学卷(解析版) 题型:解答题
(本题满分10分)设函数 .
.
(1)画出函数y=f(x)的图像;
(2)若不等式 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
查看答案和解析>>
科目:高中数学 来源:2013届湖北省仙桃市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)
设函数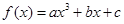
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年河北省高二下学期期末考试理科数学 题型:解答题
(本题满分10分)设 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且 ,
, 。
。
(1)当 时,求
时,求 的值.
的值.
(2)当 的面积为3时,求
的面积为3时,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com