
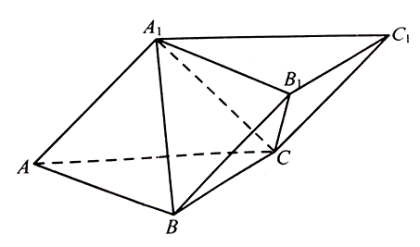
在斜三棱柱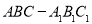 中,平面
中,平面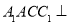 平面ABC,
平面ABC,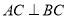 ,
,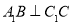 ,
,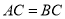 .
.
(1)求证: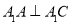 ;
;
(2)若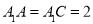 ,求三棱锥
,求三棱锥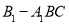 的体积.
的体积.
(1)证明过程详见解析;(2)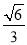 .
.
【解析】
试题分析:本题主要考查线线垂直、线面垂直、面面垂直、线线平行、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,利用面面垂直的性质得BC⊥平面A1ACC1,则利用线面垂直的性质得A1A⊥BC,由A1B⊥C1C,利用平行线A1A∥C1C,则A1A⊥A1B,利用线面垂直的判定得A1A⊥平面A1BC,则利用线面垂直的性质得A1A⊥A1C;第二问,由于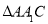 为等腰三角形,平面. A1ACC1⊥平面ABC,所以
为等腰三角形,平面. A1ACC1⊥平面ABC,所以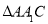 中边AC上的高为斜三棱柱
中边AC上的高为斜三棱柱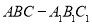 的高,而三棱锥
的高,而三棱锥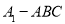 与三棱锥
与三棱锥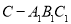 的体积相等.
的体积相等.
(1)因为平面A1ACC1⊥平面ABC,AC⊥BC,所以BC⊥平面A1ACC1,
所以A1A⊥BC.
因为A1B⊥C1C,A1A∥C1C,所以A1A⊥A1B,又BC∩A1B=B,
所以A1A⊥平面A1BC,又A1C?平面A1BC,所以A1A⊥A1C. 5分

(2)由已知及(1),△A1AC是等腰直角三角形,AA1=A1C=2,AC= .
.
因为平面A1ACC1⊥平面ABC,
所以Rt△A1AC斜边上的高等于斜三棱柱ABC-A1B1C1的高,且等于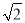 . 7分
. 7分
在Rt△ABC中,AC=BC=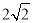 ,S△ABC=
,S△ABC=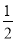 AC·BC=4,
AC·BC=4,
三棱柱ABC-A1B1C1的体积V=S△ABC· =
= . 10分
. 10分
又三棱锥A1-ABC与三棱锥C-A1B1C1的体积相等,都等于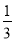 V,
V,
所以三棱锥B1-A1BC的体积V1=V-2× V=
V=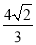 . 12分
. 12分
考点:线线垂直、线面垂直、面面垂直、线线平行、三棱锥的体积.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
已知曲线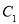 的直角坐标方程为
的直角坐标方程为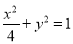 . 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线
. 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线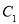 上一点,
上一点,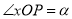 ,
,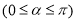 ,将点P绕点O逆时针旋转角
,将点P绕点O逆时针旋转角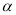 后得到点Q,
后得到点Q,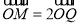 ,点M的轨迹是曲线
,点M的轨迹是曲线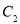 .
.
(1)求曲线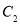 的极坐标方程;
的极坐标方程;
(2)求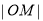 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试理科数学试卷(解析版) 题型:选择题
椭圆
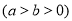 的左、右焦点为
的左、右焦点为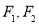 ,过
,过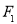 作直线
作直线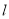 交C于A,B两点,若
交C于A,B两点,若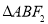 是等腰直角三角形,且
是等腰直角三角形,且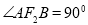 ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )
A.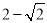 B.
B.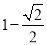 C.
C.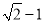 D.
D.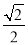
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试文科数学试卷(解析版) 题型:解答题
已知曲线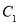 的直角坐标方程为
的直角坐标方程为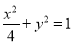 . 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线
. 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线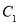 上一点,
上一点,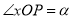 ,
, ,将点P绕点O逆时针旋转角
,将点P绕点O逆时针旋转角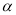 后得到点Q,
后得到点Q,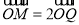 ,点M的轨迹是曲线
,点M的轨迹是曲线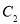 .
.
(1)求曲线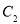 的极坐标方程;
的极坐标方程;
(2)求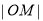 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试文科数学试卷(解析版) 题型:选择题
椭圆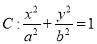
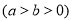 的左、右焦点为
的左、右焦点为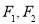 ,过
,过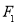 作直线
作直线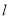 交C于A,B两点,若
交C于A,B两点,若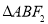 是等腰直角三角形,且
是等腰直角三角形,且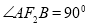 ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )
A.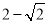 B.
B.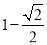 C.
C.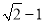 D.
D.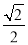
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三年级模拟考试理科数学试卷(解析版) 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
元件A | 8 | 12 | 40 | 32] | 8 |
元件B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com