
【题目】已知函数![]() ,下列命题:
,下列命题:
①![]() 的定义域为
的定义域为![]() ;
;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上单调递增;
上单调递增;
④若实数![]() 满足
满足![]() ,则
,则![]() ;
;
⑤设函数![]() 在上的最大值为
在上的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() .
.
其中真命题的序号是______.(写出所有真命题的序号)
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,焦距为2.
,焦距为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 的另一个交点为点
的另一个交点为点![]() ,与圆
,与圆![]() 的另一个交点为点
的另一个交点为点![]() ,是否存在直线
,是否存在直线![]() 使得
使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“总把新桃换旧符”(王安石)、“灯前小草写桃符”(陆游),春节是中华民族的传统节日.在宋代人们用写“桃符”的方式来祈福避祸,而现代人们通过贴“福”字、春联等方式来表达对新年的美好祝愿.某商家在春节前开展商品促销活动,顾客凡购物金额满50元,则可以任意免费领取一张“福”字或一副春联。茎叶图的统计数据是在不同时段内领取“福”字和春联的人数,则它们的中位数依次为( )
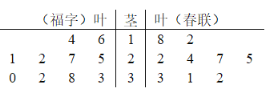
A.25,27B.26,25C.26,27D.27,25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+acosx+bx,非空数集A={x|f(x)=0},B={x|f(f(x))=0},已知A=B,则参数a的所有取值构成的集合为_____;参数b的所有取值构成的集合为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的用电情况,某地供电局抽查了该市若干户居民月均用电量(单位:![]() ),并将样本数据分组为
),并将样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示.
,其频率分布直方图如图所示.
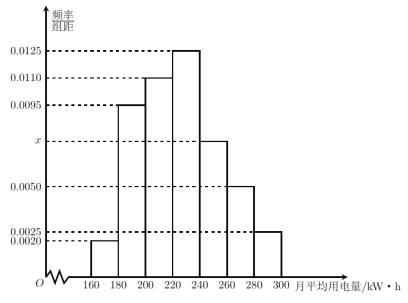
(1)若样本中月均用电量在![]() 的居民有
的居民有![]() 户,求样本容量;
户,求样本容量;
(2)求月均用电量的中位数;
(3)在月均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组居民中,用分层随机抽样法抽取
的四组居民中,用分层随机抽样法抽取![]() 户居民,则月均用电量在
户居民,则月均用电量在![]() 的居民应抽取多少户?
的居民应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面是边长为2的正方形,平面PAD⊥平面ABCD,PA⊥AD,∠PDA=45°,E,F分别为AB,PC的中点.
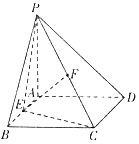
(1)证明:EF∥平面PAD;
(2)在线段BC上是否存在一点H,使平面PAH⊥平面DEF?若存在,求此时二面角C﹣HD﹣P的平面角的正切值:若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 在以
在以![]() 为圆心,1为半径的圆
为圆心,1为半径的圆![]() 上,且
上,且![]() .
.
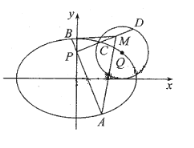
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com