
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源:不详 题型:解答题

 与函数
与函数 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;  恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围; 〔其中
〔其中 , e为自然对数的底数)
, e为自然对数的底数)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且定义域为(0,2).
,且定义域为(0,2). +3在(0,2)上的解;
+3在(0,2)上的解; 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数 的取值范围;
的取值范围; 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解 ,求k的取值范围。
,求k的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
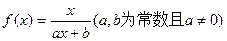 满足
满足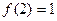 ,且
,且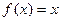 有唯
有唯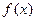 的表达式 ;
的表达式 ;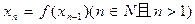 ,且
,且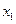 =
=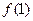 ,求数列
,求数列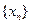 的通项公式。
的通项公式。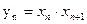 ,数列{
,数列{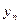 }的前
}的前 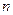 项和为
项和为 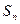 ,是否存在k∈N*,使得
,是否存在k∈N*,使得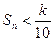
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
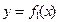 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数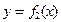 的图象与直线
的图象与直线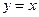 的两个交点间的距离为8,
的两个交点间的距离为8,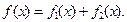
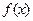 的表达式;
的表达式;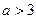 时,关于
时,关于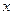 的方程
的方程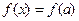 有三个实数解.
有三个实数解.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.如“函数f(x)=x3-3x2+3x对称中心为点 (1,1)”请你将这一发现
′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.如“函数f(x)=x3-3x2+3x对称中心为点 (1,1)”请你将这一发现
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com