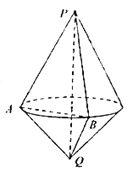
【题目】下图中的几何体是由两个有共同底面的圆锥组成．已知两个圆锥的顶点分别为P、Q，高分别为2、1，底面半径为1．A为底面圆周上的定点，B为底面圆周上的动点（不与A重合）．下列四个结论：
①三棱锥
体积的最大值为
；
②直线PB与平面PAQ所成角的最大值为
；
③当直线BQ与AP所成角最小时，其正弦值为
；
④直线BQ与AP所成角的最大值为
；
其中正确的结论有___________.（写出所有正确结论的编号）
智趣寒假作业云南科技出版社系列答案科目：高中数学 来源： 题型：
【题目】（1）求证： 
.
（2）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
sin213°＋cos217°－sin13°cos17°；
sin215°＋cos215°－sin15°cos15°；
sin218°＋cos212°－sin18°cos12°；
sin2(－18°)＋cos248°－sin(－18°)cos48°；
sin2(－25°)＋cos255°－sin(－25°)cos55°.
①试从上述五个式子中选择一个，求出这个常数；
②根据①的计算结果，将该同学的发现推广为三角恒等式．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校共有15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位:小时）
（1）应收集多少位女生样本数据？
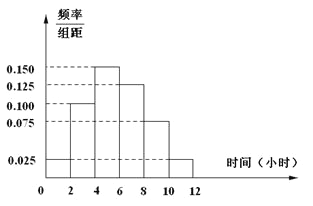
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据分组区间为：
.估计该校学生每周平均体育运动时间超过4个小时的概率.
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表，并判断是否有
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附：
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】运动员参加射击比赛,每人射击4次(每次射一发),比赛规定:全不中得0分,只中一弹得15分,中两弹得40分,中三弹得65分,中四弹得100分.已知某一运动员每一次射击的命中率为
,则他的得分期望为_____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三年级举行了一次全年级的大型考试,在数学成绩优秀和非优秀的学生中,物理、化学、总分成绩也为优秀的人数如下表所示,则我们能以99%的把握认为数学成绩优秀与物理、化学、总分成绩优秀有关系吗?
物理优秀 | 化学优秀 | 总分优秀 | |
数学优秀 | 228 | 225 | 267 |
数学非优秀 | 143 | 156 | 99 |
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱锥P－ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为
的正三角形，E，F分别是PA，AB的中点，∠CEF=90°.则球O的体积为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)=
+bx+c,
(1)若f(x)在(-∞,+∞)上是增函数,求b的取值范围;
(2)若f(x)在x=1处取得极值,且x∈[-1,2]时,f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
