
【题目】已知![]() 的最大值为A,若存在实数
的最大值为A,若存在实数![]() 使得对任意实数
使得对任意实数![]() 总有
总有![]() 成立,则
成立,则![]() 的最小值为____________
的最小值为____________
【答案】![]()
【解析】
利用三角恒等变换可得f(x)=2sin(2019x+![]() ),依题意可知A=2,|x1﹣x2|的最小值为
),依题意可知A=2,|x1﹣x2|的最小值为![]() T=
T=![]() ,从而可得答案.
,从而可得答案.
∵f(x)=sin(2019x+![]() )+cos(2019x﹣
)+cos(2019x﹣![]() ),
),
=![]() sin2019x+
sin2019x+![]() cos2019x+
cos2019x+![]() cos2019x+
cos2019x+![]() sin2019x,
sin2019x,
=![]() sin2019x+cos2019x
sin2019x+cos2019x
=2sin(2019x+![]() ),
),
∴A=f(x)max=2,周期T=![]() ,
,
又存在实数x1,x2,对任意实数x总有f(x1)≤f(x)≤f(x2)成立,
∴f(x2)=f(x)max=2,f(x1)=f(x)min=﹣2,
|x1﹣x2|的最小值为![]() T=
T=![]() ,又A=2,
,又A=2,
∴A|x1﹣x2|的最小值为![]() .
.
故答案为:![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学应用知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
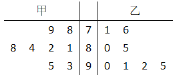
(Ⅰ)分别估计甲、乙两名同学在培训期间所有测试成绩的平均分;
(Ⅱ)从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考,求甲、乙两人成绩都在90分以上的概率;
(Ⅲ)现要从甲、乙中选派一人参加正式比赛,根据所抽取的两组数据分析,你认为选派哪位同学参加较为合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】开发商现有四栋楼A,B,C,D.楼D位于BC间,到楼A,B,C的距离分别为![]() ,
,![]() ,
,![]() ,且从楼D看楼A,B的视角为
,且从楼D看楼A,B的视角为![]() .如图所示,不计楼大小和高度.
.如图所示,不计楼大小和高度.
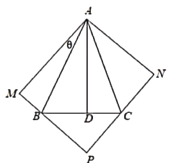
(1)试求从楼A看楼B,C视角大小;
(2)开发商为谋求更大开发区域,拟再建三栋楼M,P,N,形成以楼AMPN为顶点的矩形开发区域,规划要求楼B,C分别位于楼MP和楼PN间,如图所示,记![]() ,当
,当![]() 等于多少时,矩形开发区域面积最大?
等于多少时,矩形开发区域面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要建造一段![]() 长的高速公路,工程队需要把380名施工人员分为两组,一组负责
长的高速公路,工程队需要把380名施工人员分为两组,一组负责![]() 的软土地带的施工,另一组完成剩下的
的软土地带的施工,另一组完成剩下的![]() 硬土地带的施工.根据工程技术人员的测算,软、硬地带每米公路的工程量分别为50人·天和30人·天.
硬土地带的施工.根据工程技术人员的测算,软、硬地带每米公路的工程量分别为50人·天和30人·天.
(1)设参与软土地带工作的人数为![]() 人,试分别写出在软、硬地带筑路的时间
人,试分别写出在软、硬地带筑路的时间![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)问如何安排两组的人数,才能使全队筑路工期最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】风景秀美的宝湖畔有四棵高大的银杏树,记作A,B,P,Q,湖岸部分地方围有铁丝网不能靠近.欲测量P,Q两棵树和A,P两棵树之间的距离,现可测得A,B两点间的距离为100 m,∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,如图所示.则P,Q两棵树和A,P两棵树之间的距离各为多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
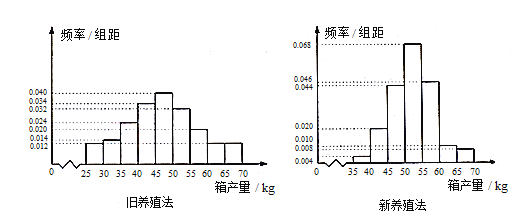
(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com