
【题目】如图,一张矩形白纸ABCD,AB=10,AD=![]() ,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)
,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)

①当平面ABE∥平面CDF时,AC∥平面BFDE
②当平面ABE∥平面CDF时,AE∥CD
③当A、C重合于点P时,PG⊥PD
④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某机构通过对某企业2018年的前三个季度生产经营情况的调查,得到每月利润![]() (单位:万元)与相应月份数
(单位:万元)与相应月份数![]() 的部分数据如表:
的部分数据如表:
| 3 | 6 | 9 |
| 241 | 244 | 229 |
(1)根据上表数据,请从下列三个函数中选取一个恰当的函数描述![]() 与x的变化关系,并说明理由:
与x的变化关系,并说明理由:![]() ,
,![]() ,
,![]()
(2)利用(1)中选择的函数:
①估计月利润最大的是第几个月,并求出该月的利润;
②预估年底12月份的利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设0<a<1,则函数f(x)=loga|![]() |( )
|( )
A.在(-∞,-1)和(1,+∞)上单调递减,在(-1,1)上单调递增
B.在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减
C.在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递增
D.在(-∞,-1)和(1,+∞)上单调递减,在(-1,1)上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度,某中学团委以问卷形式调查了![]() 位家长,得到如下统计表:
位家长,得到如下统计表:

(1)据此样本,能否有![]() 的把握认为“接受程度”与家长性别有关?说明理由;
的把握认为“接受程度”与家长性别有关?说明理由;
(2)学校决定从男性家长中按分层抽样方法选出![]() 人参加今年的高中学生成人礼仪式,并从中选
人参加今年的高中学生成人礼仪式,并从中选![]() 人交流发言,设
人交流发言,设![]() 是发言人中持“赞成”态度的人数,求
是发言人中持“赞成”态度的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据
|
|
|
|
|
|
参考公式
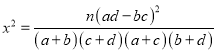
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光对物体的照度与光的强度成正比,比例系数为![]() ,与光源距离的平方成反比,比例系数为
,与光源距离的平方成反比,比例系数为![]() 均为正常数
均为正常数![]() 如图,强度分别为8,1的两个光源A,B之间的距离为10,物体P在连结两光源的线段AB上
如图,强度分别为8,1的两个光源A,B之间的距离为10,物体P在连结两光源的线段AB上![]() 不含A,
不含A,![]() 若物体P到光源A的距离为x.
若物体P到光源A的距离为x.
![]()
![]() 试将物体P受到A,B两光源的总照度y表示为x的函数,并指明其定义域;
试将物体P受到A,B两光源的总照度y表示为x的函数,并指明其定义域;
![]() 当物体P在线段AB上何处时,可使物体P受到A,B两光源的总照度最小?
当物体P在线段AB上何处时,可使物体P受到A,B两光源的总照度最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,侧棱
中,底面ABCD为正方形,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,E,F,H分别是线段PA,PD,AB的中点.
,E,F,H分别是线段PA,PD,AB的中点.
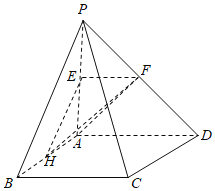
(1)求证:![]() 平面EFH;
平面EFH;
(2)求证:![]() 平面AHF;
平面AHF;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商销售某种产品,在一个销售季度内,每售出![]() 该产品获利润
该产品获利润![]() 元;未售出的产品,每
元;未售出的产品,每![]() 亏损
亏损![]() 元.根据以往的销售记录,得到一个销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
元.根据以往的销售记录,得到一个销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了![]() 该产品.用
该产品.用![]() (单位:
(单位:![]() ,
,![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该产品的利润.
(单位:元)表示下一个销售季度内经销该产品的利润.

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线y=![]() x+a没有交点,求a的取值范围;
x+a没有交点,求a的取值范围;
(3)若函数h(x)=![]() +m2x-1,x∈[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
+m2x-1,x∈[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com