
分析 设x=1+a,y=1+b,z=1+c,可得a+b+c=0.代入x3+y3+z3=3,可得:a3+b3+c3+3(a2+b2+c2)=0,利用a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ac),可得:a3+b3+c3-3abc=0.可得a2+b2+c2=-abc,且abc≤0.于是x2+y2+z2=a2+b2+c2+3=3-abc.①若a,b,c有一个为0,那么x2+y2+z2=3 (此时a=b=c=0显然满足条件).②若a,b,c有两正一负,不妨设a≥b>0>c,2(a2+ab+b2)=ab(a+b),设ab=u,a+b=v.化简整理即可得出.
解答 解:设x=1+a,y=1+b,z=1+c,∵x+y+z=3,
那么a+b+c=0.
代入x3+y3+z3=3,
可得:a3+b3+c3+3(a2+b2+c2)=0,
∵a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ac),
可得:a3+b3+c3-3abc=0.
∴a2+b2+c2=-abc,且abc≤0.
∵x2+y2+z2=a2+b2+c2+2(a+b+c)+3=a2+b2+c2+3=3-abc,
①若a,b,c有一个为0,那么x2+y2+z2=3 (此时a=b=c=0显然满足条件).
②若a,b,c有两正一负,不妨设a≥b>0>c,
2(a2+ab+b2)=ab(a+b),
设ab=u,a+b=v.
那么2v2-2u=uv,化为2v2=u(v+2),
∴u=$\frac{2{v}^{2}}{v+2}$=2(v-2)+$\frac{8}{v+2}$.
∵v=a+b>0,
∴v的可取值为2,6.
此时u为4,9.
∴a+b=2,ab=4或a+b=6,ab=9.
此时有整数解a=3,b=3,c=-6,
对应x=4,y=4,z=-5.
此时x2+y2+z2=57.
∴x2+y2+z2=57或3.
点评 本题考查了乘法公式的应用、换元方法、分类讨论方法,考查了变形能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
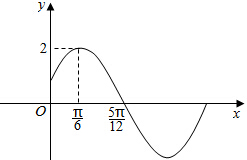 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | a>b>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3l-2m+$\frac{1}{3}n$ | B. | 3l-2m-$\frac{1}{3}n$ | C. | 3l-2m+3n | D. | 3l-2m-3n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
| 频数 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com