
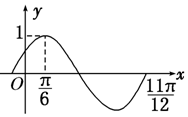
分析 由题意结合函数的图象,求出周期T,根据周期公式求出ω,求出A,根据函数的图象经过($\frac{π}{6}$,1),求出φ即可.
解答 解:由函数的图象可知:$\frac{3}{4}$T=$\frac{11π}{12}$-$\frac{π}{6}$=$\frac{3π}{4}$π,
T=π,所以ω=2,A=1,
函数的图象经过($\frac{π}{6}$,1),所以1=sin(2×$\frac{π}{6}$+φ),
因为|φ|<$\frac{π}{2}$,所以φ=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题是基础题,考查三角函数的图象与性质,函数解析式的求法,考查计算能力,发现问题解决问题的能力.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com