
如果二面角
α-l-β的平面角是锐角,过空间一点P作PA⊥α,PB⊥β,且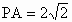 ,PB=4,点P到棱l的距离为
,PB=4,点P到棱l的距离为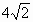 ,求此二面角的大小.
,求此二面角的大小.
|
解:由于点 P可能在二面角α-l-β内部,也可能在外部,应分两种情况进行讨论.(1)当点P在二面角α-l-β内部(如图①)时∵PA⊥α,∴PA⊥l.在α内过A作AC⊥l,此时l⊥平面PAC.同理 l⊥平面PBC.∵平面 PAC∩平面PBC=PC,∴平面 PAC与平面PBC应重合.∴∠ ABC是α-l-β的平面角.在 Rt△APC中,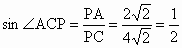 .∴∠ACP=30°. .∴∠ACP=30°.
在 Rt△BPC中,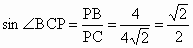 ,∴∠BCP=45° ,∴∠BCP=45°
∴∠ ACB=∠ACP+∠BCP=45°+30°=75°.(2) 当点P在二面角α-l-β外部时(如图②),同理可求∠ACB=45°-30°=15°∴二面角 α-l-β的值是75°,或15°.
|


科目:高中数学 来源: 题型:013
A.45°或30° B.15°或75°
C.30°或60° D.15°或60°
查看答案和解析>>
科目:高中数学 来源: 题型:
A.45°或30° B.15°或75° C.30°或60° D.15°或60°
查看答案和解析>>
科目:高中数学 来源: 题型:
如果二面角α-l-β的平面角是锐角,点P到α、β和棱l的距离分别为![]() ,4和
,4和![]() ,那么这个二面角的大小为( )
,那么这个二面角的大小为( )
A.45°或30° B.15°或75° C.30°或60° D.15°或60°
查看答案和解析>>
科目:高中数学 来源: 题型:
A.45°或30°B.15°或75°C.30°或60°D.15°或60°
查看答案和解析>>
科目:高中数学 来源: 题型:
A.45°或30° B.15°或75°
C.30°或60° D.15°或60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com