
 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2分析 (Ⅰ)由点E在平面ABCD内的射影恰为A,可得AE⊥平面ABCD,进一步得到平面ABCD⊥平面ABEG,又以BD为直径的圆经过A,C,AD=AB,可得BCD为正方形,再由线面垂直的性质可得BC⊥平面ABEG,从而得到EF⊥BC,结合AB=AE=GE,可得∠ABE=∠AEB=$\frac{π}{4}$,从而得到∠AEF+∠AEB=$\frac{π}{2}$,有EF⊥BE.再由线面垂直的判定可得EF⊥平面BCE,即平面EFP⊥平面BCE;
(Ⅱ)解:连接DE,由(Ⅰ)知,AE⊥平面ABCD,则AE⊥AD,又AB⊥AD,则AB⊥平面ADE,得到GE⊥平面ADE.然后利用等积法求几何体ADC-BCE的体积.
解答 (Ⅰ)证明:∵点E在平面ABCD内的射影恰为A,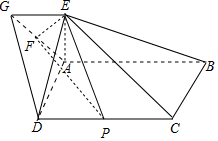
∴AE⊥平面ABCD,
又AE?平面ABEG,∴平面ABCD⊥平面ABEG,
又以BD为直径的圆经过A,C,AD=AB,∴ABCD为正方形,
又平面ABCD∩平面ABEG=AB,∴BC⊥平面ABEG,
∵EF?平面ABEG,∴EF⊥BC,
又AB=AE=GE,∴∠ABE=∠AEB=$\frac{π}{4}$,
又AG的中点为F,∴∠AEF=$\frac{π}{4}$.
∵∠AEF+∠AEB=$\frac{π}{2}$,∴EF⊥BE.
又BE?平面BCE,BC?平面BCE,BC∩BE=B,
∴EF⊥平面BCE,
又EF?平面EFP,∴平面EFP⊥平面BCE;
(Ⅱ)解:连接DE,由(Ⅰ)知,AE⊥平面ABCD,
∴AE⊥AD,又AB⊥AD,AE∩AD=A,
∴AB⊥平面ADE,又AB∥GE,∴GE⊥平面ADE.
∴VADC-BCE=${V}_{G-ADE}+{V}_{E-ABCD}=\frac{1}{3}•GE•{S}_{△ADE}$$+\frac{1}{3}•AE•{S}_{ABCD}$
=$\frac{1}{3}×2×\frac{1}{2}×2×2+\frac{1}{3}×2×2×2=4$.
∴几何体ADC-BCE的体积为4.
点评 本题主要考查点、线、面的位置关系以及体积的求法,考查运算求解能力及空间想象能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 劳动生产率为1 000元时,工人工资为130元 | |
| B. | 劳动生产率提高1 000元时,工人工资平均提高80元 | |
| C. | 劳动生产率提高1 000元时,工人工资平均提高130元 | |
| D. | 当月工资为250元时,劳动生产率为2 000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{16}{13}$ | C. | $\frac{32}{13}$ | D. | $\frac{30}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,∠A=∠B是sin∠A=sin∠B的充要条件 | |
| B. | 命题“若|x|>|y|,则x>y”的否命题是“若|x|≤|y|,则x≤y” | |
| C. | 复数(a+bi)(1+i)与复数-1+3i相等的充要条件是“a=1,b=2” | |
| D. | 命题“?x∈(0,+∞),2x>1”的否定是“?x0∈(-∞,0],2${\;}^{{x}_{0}}$≤1” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a≥$\frac{8}{9}$ | C. | a≥$\frac{7}{8}$ | D. | a≥$\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{128}$ | B. | $\frac{1}{256}$ | C. | $\frac{1}{512}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com