
 某地区在高一年级学完《数学必修1》后进行评估测试.现从所有参加测试的全体学生中随机抽取500名学生的试卷进行统计分析,就学生的成绩制成频率分布直方图(如图).
某地区在高一年级学完《数学必修1》后进行评估测试.现从所有参加测试的全体学生中随机抽取500名学生的试卷进行统计分析,就学生的成绩制成频率分布直方图(如图).分析 (1)根据频率分布直方图,求出成绩不低于80分的频率,计算出对应的频数即可;
(2)计算成绩不低于60分的频率即可;
(3)根据频率分布直方图求出频率等于0.5对应的数据值即为中位数,最高的小矩形底边的中点即为众数.
解答 解:(1)根据频率分布直方图,得;
成绩不低于80分的频率是(0.026+0.018)×10=0.44,
∴成绩不低于80分的有500×0.44=220(人);…(4分)
(2)成绩不低于60分的频率为1-0.004×10=0.96,
∴这次评估测试的合格率为0.96=96%; …(8分)
(3)∵(0.004+0.020)×10=0.24<0.5,
0.24+0.032×10=0.56>0.5,
∴中位数应在[70,80)之间,设为x,
则(x-70)×0.032+0.24=0.5,
解得x=78.1,
∴中位数为78.1;
在频率分布直方图中,最高的小矩形是70~80组,
∴这组数据的众数为$\frac{70+80}{2}$=75. …(12分)
点评 本题考查了频率分布直方图的应用问题,也考查了众数、中位数的计算问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
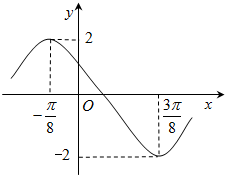 已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com