
【题目】【2017南通扬州泰州苏北四市高三二模】(本小题满分14分)
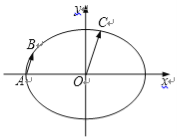
如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,C为椭
,C为椭
圆上位于第一象限内的一点.
(1)若点![]() 的坐标为
的坐标为![]() ,求a,b的值;
,求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且![]() ,求直线AB的斜率.
,求直线AB的斜率.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】公差不为零的等差数列{an}中,a3=7,又a2 , a4 , a9成等比数列.
(1)求数列{an}的通项公式.
(2)设bn=2 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() =(1,﹣2),
=(1,﹣2), ![]() =(a,﹣1),
=(a,﹣1), ![]() =(﹣b,0)(a>0,b>0,O为坐标原点),若A、B、C三点 共线,则
=(﹣b,0)(a>0,b>0,O为坐标原点),若A、B、C三点 共线,则 ![]() 的最小值是( )
的最小值是( )
A.4
B.![]()
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分16分)
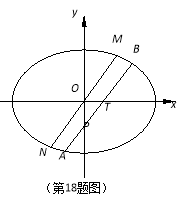
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:+=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求的值;
(3)记直线l与y轴的交点为P.若=,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到面对角线BC1的距离相等,则点P的轨迹是( )
A.线段
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
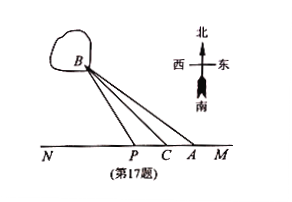
【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图,已知![]() 两镇分别位于东西湖岸
两镇分别位于东西湖岸![]() 的
的![]() 处和湖中小岛的
处和湖中小岛的![]() 处,点
处,点![]() 在
在![]() 的
的
正西方向![]() 处,
处,![]() .现计划铺设一条电缆联通
.现计划铺设一条电缆联通![]() 两镇,有
两镇,有
两种铺设方案:①沿线段![]() 在水下铺设;②在湖岸
在水下铺设;②在湖岸![]() 上选一点
上选一点![]() ,先沿线段
,先沿线段![]() 在地
在地
下铺设,再沿线段![]() 在水下铺设,预算地下、水下的电缆铺设费用分别为
在水下铺设,预算地下、水下的电缆铺设费用分别为![]() 万元∕
万元∕![]() 、
、
![]() 万元∕
万元∕![]() .
.
(1)求![]() 两镇间的距离;
两镇间的距离;
(2)应该如何铺设,使总铺设费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前项和为Sn , 且Sn= ![]() ,{bn}为等差数列,且a1=b1 , a2(b2﹣b1)=a1 .
,{bn}为等差数列,且a1=b1 , a2(b2﹣b1)=a1 .
(1)求数列{an}和{bn}通项公式;
(2)设 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1(﹣c,0)、F2(c,0)是椭圆 ![]() =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1 , 则椭圆的离心率为( )
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com