
【题目】(本题满分12分)已知椭圆C: ![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆的两个焦点,
是椭圆的两个焦点, ![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的周长是
的周长是![]() .
.
(1)求椭圆C的方程;
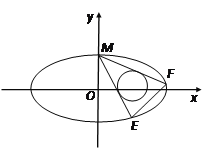
(2)设圆T: ![]() ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在![]() 轴上移动且
轴上移动且![]() 时,求EF的斜率的取值范围.
时,求EF的斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由椭圆离心率得到a,c的关系,再由△PF1F2的周长是8+2![]() 得a,c的另一关系,联立求得a,c的值,代入隐含条件求得b,则椭圆方程可求;(2)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,由圆心到切线距离等于半径得到关于切线斜率的方程,由根与系数关系得到
得a,c的另一关系,联立求得a,c的值,代入隐含条件求得b,则椭圆方程可求;(2)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,由圆心到切线距离等于半径得到关于切线斜率的方程,由根与系数关系得到
![]() ,再联立一切线方程和椭圆方程,求得E的坐标,同理求得F坐标,另一两点求斜率公式得到
,再联立一切线方程和椭圆方程,求得E的坐标,同理求得F坐标,另一两点求斜率公式得到![]() .然后由函数单调性求得EF的斜率的范围
.然后由函数单调性求得EF的斜率的范围
试题解析:(1)由![]() ,即
,即![]() ,可知a=4b,
,可知a=4b, ![]() ,
,
∵△PF1F2的周长是![]() ,
,
∴![]() ,∴a=4,b=1,所求椭圆方程为
,∴a=4,b=1,所求椭圆方程为![]() ;
;
(2)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,
由直线y=kx+1与T相切可知![]() ,
,
即(9t2﹣4)k2+18tk+5=0,
∴![]() ,
,
由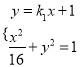 ,得
,得![]() .
.
∴![]() , 同理
, 同理![]() ,
,
则![]() .
.
当1<t<3时, ![]() 为增函数,故EF的斜率的范围为
为增函数,故EF的斜率的范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 的
的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出定义:若 m﹣ ![]() <x≤m+
<x≤m+ ![]() (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=x﹣{x}的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=x﹣{x}的四个命题:
①函数y=f(x)的定义域是R,值域是(﹣ ![]() ,
, ![]() ]
]
②函数y=f(x)的图象关于y轴对称;
③数y=f(x)的图象关于坐标原点对称;
④函数y=f(x)在(﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
则其中正确命题是(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com