
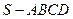
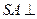

 平面SAP;
平面SAP;
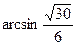
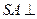 底面
底面 ,
,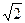 ,…………………………………….…..………….2分
,…………………………………….…..………….2分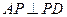 .………….…….3分
.………….…….3分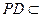 平面ABCD,
平面ABCD, 平面SAP. …………………………….5分
平面SAP. …………………………….5分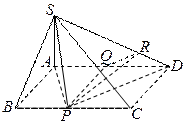 由于SA⊥底面ABCD,且SA
由于SA⊥底面ABCD,且SA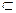 平面SAD,则平面SAD⊥平面PAD……..7分
平面SAD,则平面SAD⊥平面PAD……..7分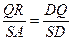
 ,所以
,所以 ….……….10分
….……….10分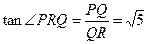 ………11分
………11分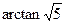 .……………….…….…….12分
.……………….…….…….12分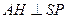 ,且垂足为H,在平面SAD内作
,且垂足为H,在平面SAD内作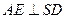 ,且垂足为E,连接HE,
,且垂足为E,连接HE,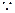
 平面SAP。
平面SAP。
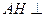 平面SDP…………7分
平面SDP…………7分
 是二面角A-SD-P的平面角……………………………….9分
是二面角A-SD-P的平面角……………………………….9分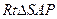 中,
中,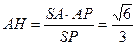 ,在
,在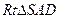 中,
中,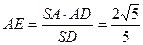 ,
,
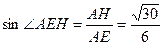 . ………………………………….11分
. ………………………………….11分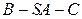 的大小为
的大小为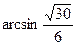 ……………………………12分
……………………………12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com