练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-2-10,已知半圆的直径AB =6 cm,CD是半圆上长为2 cm的弦,AC与BD延长线交于P,当弦CD在半圆上滑动时,求证:∠P为定值,并求出这个定角的正弦值.

    图2-2-10

    思路分析:要证∠P为定值,考虑求出∠P的三角函数值,因此,构造以∠P为内角的直角三角形,注意到AB为直径,则连结BC、AD均可得到直角三角形.

    解:连结BC,∵CD为定长,圆直径为定值,?

    ∴在CD滑动过程中,CD的度数不变,?

    ∴∠PBC为定值.?

    又AB为直径,∴∠ACB =∠PCB=90°,?

    ∴∠P =90°-∠PBC为定值.?

    ∵∠PCD =∠PBA,∴△PCD∽△PBA.?

    ∴.?

    在Rt△PBC中,cosP =,?

    ∴sinP =.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图1-2-10,已知△ABC中,DE∥BC,CD、BE交于点O,连结AO并延长交BC于点F,AO交DE于点G.求证:=.

    图1-2-10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-2-10,已知△ABC中,D、E分别为AB、AC上的点,DE∥BC,DE=1,BC=3,AB=6,则AD的长为 (    )

    图1-2-10

    A.1             B.1.5                  C.2               D.2.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某中学举办电脑知识竞赛，满分为100分，80分以上为优秀(含80分).现将高一两个班参赛学生的成绩进行整理后分成5组，绘制成频率分布直方图如图2-2-10所示：

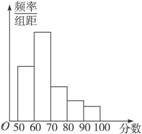
    图2-2-10

    已知图中从左到右的第一、三、四、五小组的频率分别为0.30、0.15、0.10、0.05,而第二小组的频数是40，则参赛的人数是_____，成绩优秀的频率是_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-2-10,已知点P为△ABC所在平面外任一点,点D,E,F分别在射线PA,PB,PC上,并且.

    图2-2-10

    求证:平面DEF∥平面ABC.

    查看答案和解析>>

    同步练习册答案