
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
【答案】
(1)解:由方程x2+y2+2x﹣4y+3=0知(x+1)2+(y﹣2)2=2,所以圆心为(﹣1,2),半径为 ![]() .
.
当切线过原点时,设切线方程为y=kx,则 ![]() =
= ![]() ,所以k=2±
,所以k=2± ![]() ,即切线方程为y=(2±
,即切线方程为y=(2± ![]() )x.
)x.
当切线不过原点时,设切线方程为x+y=a,则 ![]() =
= ![]() ,所以a=﹣1或a=3,即切线方程为x+y+1=0或x+y﹣3=0.
,所以a=﹣1或a=3,即切线方程为x+y+1=0或x+y﹣3=0.
综上知,切线方程为y=(2± ![]() )x或x+y+1=0或x+y﹣3=0;
)x或x+y+1=0或x+y﹣3=0;
(2)解:因为|PO|2+r2=|PC|2,所以x12+y12+2=(x1+1)2+(y1﹣2)2,即2x1﹣4y1+3=0.
要使|PM|最小,只要|PO|最小即可.
当直线PO垂直于直线2x﹣4y+3=0时,即直线PO的方程为2x+y=0时,|PM|最小,
此时P点即为两直线的交点,得P点坐标(﹣ ![]() ,
, ![]() ).
).
【解析】(1)将圆的一般方程转化为标准方程,得到圆心坐标和半径,分切线过原点和不过原点进行设直线方程,再通过圆心到切线方程的距离等于半径即可得出切线方程,(2)在直角三角形PMC中,根据勾股定理可得|PM|2+|CM|2=|PC|2,由|PM|=|PO|,|CM|=r可得|PO|2+r2=|PC|2,由两点间距离公式经化简可得2x1﹣4y1+3=0,要使|PM|最小,只要|PO|最小即可,当直线PO垂直于直线2x﹣4y+3=0时,即直线PO的方程为2x+y=0时,|PM|最小,可得出P点坐标.


科目:高中数学 来源: 题型:
【题目】已知 m>1 且关于 x 的不等式![]() 的解集为 [0,4] .
的解集为 [0,4] .
①求 m 的值;
②若 a , b 均为正实数,且满足 a+b=m ,求 a2+b2 的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB=AC=AA1 , ![]() ,点D是BC的中点.
,点D是BC的中点.
(I)求证:AD⊥平面BCC1B1;
(II)求证:A1B∥平面ADC1;
(III)求二面角A﹣A1B﹣D的余弦值.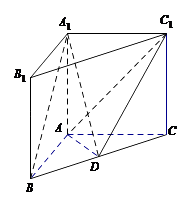
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,关于x的方程[f(x)]2+mf(x)﹣1=0有三个不同的实数解,则实数m的取值范围是( )
,关于x的方程[f(x)]2+mf(x)﹣1=0有三个不同的实数解,则实数m的取值范围是( )
A.(﹣∞,e﹣ ![]() )
)
B.(e﹣ ![]() ,+∞)
,+∞)
C.(0,e)
D.(1,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为对本公司的160名员工的身体状况进行调查,先将员工随机编号为1,2,3,…,159,160,采用系统抽样的方法(等间距地抽取,每段抽取一个个体)将抽取的一个样本.已知抽取的员工中最小的两个编号为5,21,那么抽取的员工中,最大的编号应该是( )
A.141
B.142
C.149
D.150
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)后得到如图所示的频率分布直方图.
(1)求这40名学生中数学成绩不低于120分的学生人数;
(2)若从数学成绩[80,100)内的学生中任意抽取2人,求成绩在[80,90)中至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,其中a10=30,a20=50.
(1)求数列{an}的通项公式;
(2)若bn=an﹣20,求数列{bn}的前n项和Tn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 且函数y=f(x)图象上点(1,f(1))处的切线斜率为0.
且函数y=f(x)图象上点(1,f(1))处的切线斜率为0.
(1)试用含有a的式子表示b,并讨论f(x)的单调性;
(2)对于函数图象上的不同两点A(x1 , y1),B(x2 , y2)如果在函数图象上存在点M(x0 , y0),(x0∈(x1 , x2))使得点M处的切线l∥AB,则称AB存在“跟随切线”.特别地,当 ![]() 时,又称AB存在“中值跟随切线”.试问:函数f(x)上是否存在两点A,B使得它存在“中值跟随切线”,若存在,求出A,B的坐标,若不存在,说明理由.
时,又称AB存在“中值跟随切线”.试问:函数f(x)上是否存在两点A,B使得它存在“中值跟随切线”,若存在,求出A,B的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(n)=(1+ ![]() )n﹣n,其中n为正整数.
)n﹣n,其中n为正整数.
(1)求f(1),f(2),f(3)的值;
(2)猜想满足不等式f(n)<0的正整数n的范围,并用数学归纳法证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com