练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设是首项为1的正项数列，且（=1，2，3，…），则它的通项公式是=________。

    1/n

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    有n（n≥3，n∈N*）个首项为1，项数为n的等差数列，设其第m（m≤n，m∈N*）个等差数列的第k项为amk（k=1，2，3，…，n），且公差为dm．若d1=1，d2=3，a1n，a2n，a3n，…，ann也成等差数列．
    （Ⅰ）求dm（3≤m≤n）关于m的表达式；
    （Ⅱ）将数列dm分组如下：（d1），（d2，d3，d4），（d5，d6，d7，d8，d9）…，（每组数的个数组成等差数列），设前m组中所有数之和为（cm）4（cm＞0），求数列{2cmdm}的前n项和Sn；
    （Ⅲ）设N是不超过20的正整数，当n＞N时，对于（Ⅱ）中的Sn，求使得不等式
    150
    (Sn-6)＞dn    成立的所有N的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2007上海，20)如果有穷数列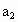，，，…，(n为正整数)满足条件即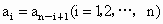，我们称其为“对称数列”．例如，由组合数组成的数列就是“对称数列”．

    (1)设是项数为7的“对称数列”，其中是等差数列，且．依次写出的每一项；

    (2)设是项数为2k－1(正整数k＞1)的“对称数列”，且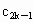，，…，是首项为50，公差为－4的等差数列．记各项的和为．当k为何值时，取得最大值?并求出的最大值；

    (3)对于确定的正整数m＞1，写出所有项数不超过2m的“对称数列”，使得依次是该数列中连续的项；当m＞1500时，求其中一个“对称数列”前2008项的和．

    查看答案和解析>>

    科目：高中数学 来源：江苏省扬州中学2012届高三最后冲刺热身数学试题 题型：044

    有n个首项都是1的等差数列，设第m个数列的第k项为a(m，k)(其中m，k＝1，2，3，···，n，n≥3)，公差为dm，并且a(1，n)，a(2，n)，a(3，n)，···，a(n，n)成等差数列．

    (1)证明：dm＝p1d1＋p2d2(3≤m≤n，p1，p2是m的多项式)，并求p1＋p2的值；

    (2)当d1＝1，d2＝3时，将数列{dm}分组如下：(d1)，(d2，d3，d4)，(d5，d6，d7，d8，d9)，…(每组数的个数构成等差数列)．设前m组中所有数之和为(cm)4(cm＞0)，求数列{2cm·dm}的前n项和Sn；

    (3)设N是不超过20的正整数，当n＞N时，对于(1)中的Sn，求使得不等式(Sn－6)＞dn成立的所有N的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

     （08年扬州中学）  如果有穷数列（为正整数）满足条件，，…，，即（），我们称其为“对称数列”．例如，由组合数组成的数列就是“对称数列”．

    （1）设是项数为7的“对称数列”，其中是等差数列，且，．依次写出的每一项；

    （2）设是项数为(正整数)的“对称数列”，其中是首项为，公差为的等差数列．记各项的和为．当为何值时，取得最大值？并求出的最大值；

        （3）对于确定的正整数，写出所有项数不超过的“对称数列”，使得依次是该数列中连续的项；当时，求其中一个“对称数列”前项的和

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如果有穷数列为正整数）满足条件

    即我们称其为“对称数列”，例如，由组合数组成的数列就是“对称数列”。

    (1) 设是项数为5的“对称数列”.其中是等差数列,且,依次写出的每一项.

    (2)设是项数为9的“对称数列”,其中是首项为1,公比为2的等比数列,求各项的和.

    (3)设是项数为(正整数的“对称数列”,其中是首项为50,公差为-4的等差数列,记的各项的和为,当为何值时, 有最大值?

    查看答案和解析>>

    同步练习册答案