
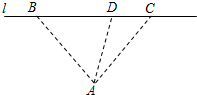
 某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=
某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=| π |
| 2 |
| 2 |
π-
| ||
| 2 |
| π |
| 4 |
| AD | ||
sin
|
| AB |
| sinα |
| 10 |
| sinα |
| BD | ||
sin[π-(α+
|
| AB |
| sinα |
10
| ||||
| sinα |
10
| ||||
| sinα |
| 10 |
| sinα |
10
| ||||
| sinα |
10
| ||||
| sinα |
1000-500
| ||||
| sinα |
| π |
| 4 |
| 3π |
| 4 |
1000-500
| ||||
| sinα |
| 2-cosα |
| sinα |
| 2-cosα |
| sinα |
| sinα•sinα-cosα(2-cosα) |
| sin2α |
| 1-2cosα |
| sin2α |
| 1 |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 3π |
| 4 |
| π |
| 3 |
2-
| ||||
|
| 3 |
| 3 |
| π |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
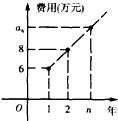 为保护环境,绿色出行,某高校今年年初成立自行车租赁公司,初期投入36万元,建成后每年收入25万元,该公司第n年需要付出的维修费用记作an万元,已知{an}为等差数列,相关信息如图所示.
为保护环境,绿色出行,某高校今年年初成立自行车租赁公司,初期投入36万元,建成后每年收入25万元,该公司第n年需要付出的维修费用记作an万元,已知{an}为等差数列,相关信息如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
| ||
| 2 |
| a |
| b |
| b |
| π |
| 3 |
| a |
| b |
| A、①④ | B、③④ | C、①③ | D、②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com