
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
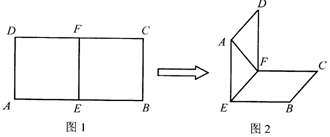
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4] | B. | [1,4) | C. | [1,4)∪(4,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
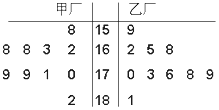 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分不必要条件 | |
| B. | 命题“若a∈M,则b∉M”的否命题是“若a∉M,则b∈M” | |
| C. | “|a|>|b|”是“a2>b2”的必要不充分条件 | |
| D. | 命题“若a,b都是奇数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a,b都不是奇数” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com