
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,以这50天的送货单数为样本,将频率视为概率,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(1)![]() ;
; ;(2)答案不唯一,具体见解析,见解析
;(2)答案不唯一,具体见解析,见解析
【解析】
(1)根据题意,找出关系,可以得出![]() ,而
,而![]() 是分段函数,根据题意,分段找关系,得到结果;
是分段函数,根据题意,分段找关系,得到结果;
(2)根据题意,得出两个公司快递员的日工资的期望分别为106元和![]() 元,比较大小得出结果(随着
元,比较大小得出结果(随着![]() 的变化而变化).
的变化而变化).
(1)甲快递公司的“快递员”的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式为
的函数关系式为![]() ;
;
乙快递公司的“快递员”的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式为
的函数关系式为
 .
.
(2)①记甲快递公司的“快递员”的日工资为X(单位:元),由题中表格易知![]() 的所有可能取值为90,100,110,120,
的所有可能取值为90,100,110,120,
则![]() ;
;![]() ;
;
![]() ;
;![]() .
.
所以![]() 的分布列为
的分布列为
| 90 | 100 | 110 | 120 |
|
|
|
|
|
故![]() (元).
(元).
②乙快递公司的快递员这50天的工资和为:(6+14)×80+24×[80+(50-40)t]+6[80+(60-40)t]=4000+360t(元),
所以乙快递公司的“快递员”的日平均工资为![]() (元),
(元),
由①知,甲快递公司的“快递员”的日平均工资为![]() 元.
元.
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ;
;
乙公司每日超过![]() 单的部分每单抽成是
单的部分每单抽成是![]() 元,
元,
当t小于![]() 元时,小赵应选择甲快递公司.
元时,小赵应选择甲快递公司.
当t等于![]() 元时,小赵选择甲、乙快递公司一样.
元时,小赵选择甲、乙快递公司一样.
当t大于![]() 元时,小赵应选择乙快递公司.
元时,小赵应选择乙快递公司.


科目:高中数学 来源: 题型:
【题目】如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
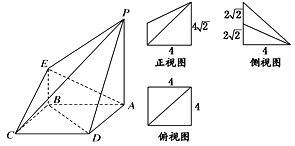
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)线段BC上是否存在点M,使得AE⊥PM?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
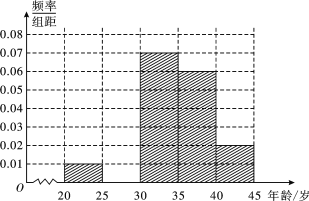
分组(单位:岁) | 频数 | 频率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合计 |
|
|
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求满足要求的那几项;若不存在,说明理由.
中的一项?若存在,求满足要求的那几项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高职工的健身意识,鼓励大家加入健步运动,要求200名职工每天晚上9:30上传手机计步截图,对于步数超过10000的予以奖励.图1为甲乙两名职工在某一星期内的运动步数统计图,图2为根据这星期内某一天全体职工的运动步数做出的频率分布直方图.
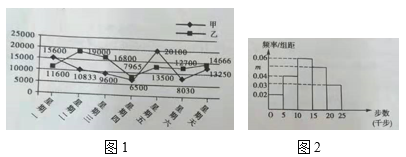
(1)在这一周内任选两天检查,求甲乙两人两天全部获奖的概率;
(2)请根据频率分布直方图,求出该天运动步数不少于15000的人数,并估计全体职工在该天的平均步数;
(3)如果当天甲的排名为第130名,乙的排名为第40名,试判断做出的是星期几的频率分布直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ).在以
).在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(Ⅰ)求![]() ,
,![]() 的值及曲线
的值及曲线![]() 和
和![]() 极坐标方程;
极坐标方程;
(Ⅱ)求![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com