
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 的图象在
的图象在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求解出导函数,根据导函数在![]() 的值为
的值为![]() 即可计算出
即可计算出![]() 的值;
的值;
(2)解法一:采用分类讨论的思想分析![]() 时
时![]() 的取值范围,确定出最小值;解法二:采用参变分离的思想分析问题,构造新函数,利用新函数的最值与
的取值范围,确定出最小值;解法二:采用参变分离的思想分析问题,构造新函数,利用新函数的最值与![]() 的关系求解出
的关系求解出![]() 的最小值.
的最小值.
(1)![]() 依题意
依题意![]() 故
故![]() ;
;
(2)解法一: ![]()
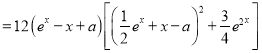 ,
,
显然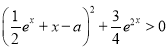 ,令
,令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 单调递增,且
单调递增,且![]() ,
,
当![]() 即
即![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
故![]() 等价于
等价于![]() ,此式已成立,从而
,此式已成立,从而![]() 满足条件,
满足条件,
当![]() 即
即![]() 时,由
时,由![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,![]() ,
,
故![]() 使得
使得![]() ,即
,即![]() ,
,
令![]() ,即
,即![]() ,得
,得![]() ,
,
又令![]() ,即
,即![]() ,得
,得![]() ,因此
,因此![]() 在
在![]() 处取得最小值,
处取得最小值,
![]() ,又
,又![]() ,故
,故![]() ,
,
设![]() ,
,![]() ,且
,且![]() ,
,
法一:![]() ,故
,故![]() 在
在![]() 单调递减,由
单调递减,由![]() 知
知![]() ,
,
即![]() ,
,![]() 而
而![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,即
,即![]() ;
;
法二:![]() ,由
,由![]() 知
知![]() ,即
,即![]() 下同法一;
下同法一;
综上可知![]() ,因此
,因此![]() 的最小值为
的最小值为![]() ;
;
解法二:当![]() 时,
时,![]() 恒成立,因求
恒成立,因求![]() 的最小值,不妨设
的最小值,不妨设![]() ,
,
则只研究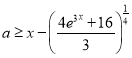 ,设
,设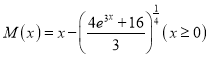 ,下求
,下求![]() ;
;
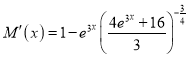 ,由
,由![]() ,并记
,并记![]() ,
,![]() ,
,
即![]() ,亦即
,亦即![]() ,
,
故![]() ,因此
,因此![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以![]() ,即
,即![]() ,因此
,因此![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某无缝钢管厂只生产甲、乙两种不同规格的钢管,钢管有内外两个口径,甲种钢管内外两口径的标准长度分别为![]() 和
和![]() ,乙种钢管内外两个口径的标准长度分别为
,乙种钢管内外两个口径的标准长度分别为![]() 和
和![]() .根据长期的生产结果表明,两种规格钢管每根的长度
.根据长期的生产结果表明,两种规格钢管每根的长度![]() 都服从正态分布
都服从正态分布![]() ,长度在
,长度在![]() 之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
(1)在该钢管厂生产的钢管中随机抽取10根进行检测,求至少有1根为废品的概率;
(2)监管部门规定每种规格钢管的“口径误差”的计算方式为:若钢管的内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() ,则“口径误差”为
,则“口径误差”为![]() ,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是![]() (正品钢管中没有“口径误差”大于
(正品钢管中没有“口径误差”大于![]() 的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
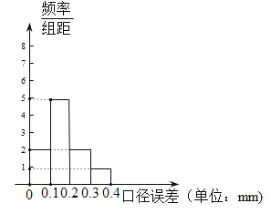

甲种钢管 乙种钢管
已知经销商经销甲种钢管,其中“一级品”的利润率为0.3,“二级品”的利润率为0.18,“合格品”的利润率为0.1;经销乙种钢管,其中“一级品”的利润率为0.25,“二级品”的利润率为0.15,“合格品”的利润率为0.08,若视频率为概率.
(ⅰ)若经销商对甲、乙两种钢管各进了100万元的货,![]() 和
和![]() 分别表示经销甲、乙两种钢管所获得的利润,求
分别表示经销甲、乙两种钢管所获得的利润,求![]() 和
和![]() 的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
(ⅱ)若经销商计划对甲、乙两种钢管总共进100万元的货,则分别在甲、乙两种钢管上进货多少万元时,可使得所获利润的方差和最小?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合)已知
是椭圆上一动点(与左、右顶点不重合)已知![]() 的内切圆半径的最大值为
的内切圆半径的最大值为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究不同性别在处理多任务时的表现差异,召集了男女志愿者各200名,要求他们同时完成多个任务,包括解题、读地图、接电话.下图表示了志愿者完成任务所需的时间分布.以下结论,对志愿者完成任务所需的时间分布图表理解正确的是( )

①总体看女性处理多任务平均用时更短;
②所有女性处理多任务的能力都要优于男性;
③男性的时间分布更接近正态分布;
④女性处理多任务的用时为正数,男性处理多任务的用时为负数.
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点
的左顶点 ![]() 与上顶点
与上顶点![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程和焦点的坐标;
的方程和焦点的坐标;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,若
,若![]() 为等边三角形,求点
为等边三角形,求点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共1000名男生中随机抽取50人测量身高,据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
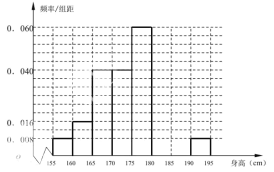
(1)求第六组、第七组的频率,并估计高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)学校决定让这五十人在运动会上组成一个高旗队,在这五十人中要选身高在![]() 以上(含
以上(含![]() )的两人作为队长,求这两人在同一组的概率.
)的两人作为队长,求这两人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且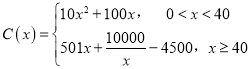 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: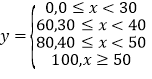 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
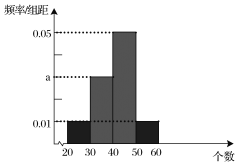
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为
的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为![]() .
.
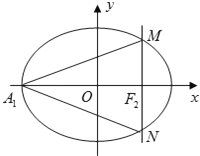
(Ⅰ)求椭圆的离心率;
(Ⅱ)若△A1MN的外接圆在M处的切线与椭圆相交所得弦长为![]() ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com