已知函数f(x)=16x3-20ax2+8a2x-a3,其中a≠0.
(1)求函数f(x)的极大值和极小值;
(2)设(1)问中函数取得极大值的点为P(x,y),求点P的轨迹方程.
解:(1)∵f(x)=16x
3-20ax
2+8a
2x-a
3,其中a≠0,
∴f'(x)=48x
2-40ax+8a
2=8(2x-a)(3x-a)
由f′(x)=0,得

,
当a>0时,

,见下表:
| x | 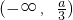 |  | 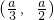 |  | 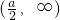 |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增函数 | 极大 | 减函数 | 极小 | 增函数 |
∴当
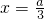
时,函数取得极大值为
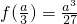
;
当
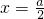
时,函数取得极小值为

当a<0时,
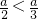
,见下表:
| x |  |  | 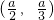 |  | 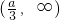 |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增函数 | 极大 | 减函数 | 极小 | 增函数 |
∴当
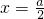
时,函数取得极大值为

;
当
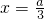
时,函数取得极小值为
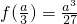
,
(2)由(1)可知:
当a>0时,
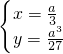
,消去a得:y=x
3(x>0),
当a<0时,
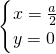
,消去a得:y=0(x<0),
所以 P点的轨迹方程为:
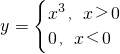
.
分析:(1)由f(x)=16x
3-20ax
2+8a
2x-a
3,知f'(x)=48x
2-40ax+8a
2=8(2x-a)(3x-a),由f′(x)=0,得

,由此能求出函数f(x)的极大值和极小值.
(2)由(1)可知:当a>0时,y=x
3(x>0);当a<0时,y=0(x<0),由此能求出P点的轨迹方程.
点评:本题考查函数的极值的求法和点的轨迹方程的应用,解题时要认真审题,仔细解答,注意导数性质和分类讨论思想的灵活运用.

 ,
, ,见下表:
,见下表: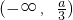

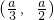

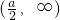
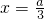 时,函数取得极大值为
时,函数取得极大值为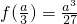 ;
;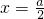 时,函数取得极小值为
时,函数取得极小值为
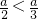 ,见下表:
,见下表:

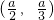

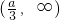
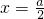 时,函数取得极大值为
时,函数取得极大值为 ;
;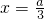 时,函数取得极小值为
时,函数取得极小值为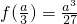 ,
,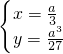 ,消去a得:y=x3(x>0),
,消去a得:y=x3(x>0),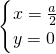 ,消去a得:y=0(x<0),
,消去a得:y=0(x<0),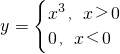 .
. ,由此能求出函数f(x)的极大值和极小值.
,由此能求出函数f(x)的极大值和极小值.
