
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60° 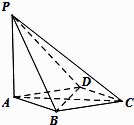
(1)若PA=AB,求PB与平面PDC所成角的正弦值;
(2)当平面PBC与平面PDC垂直时,求PA的长.
【答案】
(1)解:设AC∩BD=O,∵在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°
∴BO=1,AO=CO= ![]() ,
,
如图,以O为坐标原点,建立空间直角坐标系O﹣xyz,
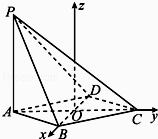
则 P(0,﹣ ![]() ,2),A(0,﹣
,2),A(0,﹣ ![]() ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0, ![]() ,0),D(﹣1,0,0)
,0),D(﹣1,0,0)
∴ ![]() =(1,
=(1, ![]() ,﹣2),
,﹣2), ![]() =(﹣1,
=(﹣1, ![]() ,﹣2),
,﹣2), ![]() =(0,2
=(0,2 ![]() ,﹣2),
,﹣2),
设平面PDC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 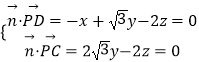 ,取y=
,取y= ![]() ,得
,得 ![]() =(﹣3,
=(﹣3, ![]() ,3),
,3),
设PB与平面PDC所成角为θ,
则sinθ ![]() =
= ![]() =
= ![]() .
.
∴PB与平面PDC所成角的正弦值为 ![]()
(2)解:由(1)知 ![]() =(﹣1,
=(﹣1, ![]() ,0),设P(0,﹣
,0),设P(0,﹣ ![]() ,t)(t>0),
,t)(t>0),
则 ![]() =(﹣1,﹣
=(﹣1,﹣ ![]() ,t),设平面PBC的法向量
,t),设平面PBC的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取y=
,取y= ![]() ,得
,得 ![]() =(3,
=(3, ![]() ,
, ![]() ),
),
同理,平面PDC的法向量 ![]() =(﹣3,
=(﹣3, ![]() ,
, ![]() ),
),
∵平面PCB⊥平面PDC,∴ ![]() =﹣9+3+
=﹣9+3+ ![]() =0,
=0,
解得t= ![]() ,∴PA=
,∴PA= ![]() .
.
【解析】(1)设AC∩BD=O,以O为坐标原点,建立空间直角坐标系O﹣xyz,利用向量法能求出PB与平面PDC所成角的正弦值.(2)求出平面PBC的法向量和平面PDC的法向量,利用向量法能求出PA的长.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则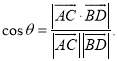 .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则 ![]() 的值为( )
的值为( )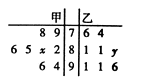
A.9
B.10
C.11
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣∞,﹣3)∪(0,3)
B.(﹣∞,﹣3)∪(3,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣3,0)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0,
(1)求l2的方程,使得:①l2与l1平行,且过点(﹣1,3); ②l2与l1垂直,且l2与两坐标轴围成的三角形面积为4;
(2)直线l1与两坐标轴分别交于A、B 两点,求三角形OAB(O为坐标原点)内切圆及外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2},B={x|(x2+ax)(x2+ax+2)=0},记集合A中元素的个数为n(A),定义m(A,B)= ![]() ,若m(A,B)=1,则正实数a的值是 .
,若m(A,B)=1,则正实数a的值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: (Ⅰ) EF∥平面A1BC1;
(Ⅱ) 平面AEF⊥平面BCC1B1 . 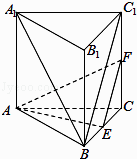
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣3=0.
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于A(x1 , y1)、B(x2 , y2)两点,求证: ![]() 为定值;
为定值;
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使△CDE的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 ![]() ,通过对被抽取学生的问卷调查,得到如下2x2列联表:
,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(Ⅰ)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(Ⅱ)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2= ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com