
| A. | 因为f(0)?f(2)>0,所以f(x)在(0,2)内没有零点 | |
| B. | 因为1是f(x)的一个零点,所以f(0)?f(2)<0 | |
| C. | 由于f(x)在区间(-∞,0)上单调递减,所以f(x)在(-∞,0)内有唯一的一个零点 | |
| D. | 以上说法都不对 |
分析 求得f(x)的零点为1,可判断A;由f(x)在(0,2)不单调,可判断B;由图象在(-∞,0)内可能与x轴没有交点,可判断C,进而得到结论.
解答 解:函数f(x)=x2-2x+1的零点,
即为f(x)=(x-1)2=0,解得x=1,即零点为1.
对A,因为f(0)•f(2)>0,所以f(x)在(0,2)内没有零点,
错误,还要考虑(0,2)内的某个函数值的符号,比如f(1)=0;
对B,因为1是f(x)的一个零点,所以f(0)•f(2)<0,
错误,要考虑(0,2)的单调性,事实上,f(0)•f(2)>0;
对C,由于f(x)在区间(-∞,0)上单调递减,
所以f(x)在(-∞,0)内有唯一的一个零点.
错误,图象在(-∞,0)内与x轴没有交点.
故选:D.
点评 本题考查函数的零点问题,以及函数零点定理的运用,注意结合图象与x轴的关系,考查判断能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
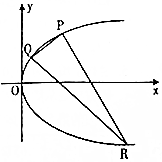 已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.
已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
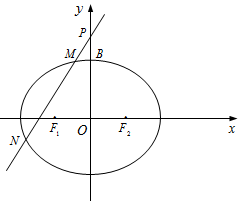 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行平移$\frac{π}{2}$个单位长度 | B. | 向右平行平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平行平移$\frac{π}{2}$个单位长度 | D. | 向左平行平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com