
【题目】关于函数![]() ,下列说法正确的是________.
,下列说法正确的是________.
①![]() 是
是![]() 的最大值点.
的最大值点.
②函数![]() 有且只有1个零点.
有且只有1个零点.
③存在正实数![]() ,使得
,使得![]() 恒成立.
恒成立.
④对任意两个不相等的正实数![]() ,若
,若![]() ,则
,则![]() .
.
【答案】②④
【解析】
①对函数求导,结合函数极值的定义进行判断即可;
②求函数的导数,结合函数单调性及零点存在性定理,可判断出零点个数;
③利用参数分离法,构造函数![]() ,求函数的导数,研究函数的单调性和极值进行判断即可;
,求函数的导数,研究函数的单调性和极值进行判断即可;
④设![]() ,则
,则![]() ,构造函数并结合函数的单调性,可证明
,构造函数并结合函数的单调性,可证明![]() ,再结合
,再结合![]() 的单调性,可得到
的单调性,可得到![]() ,即可得到
,即可得到![]() .
.
对于①,![]() 的定义域为
的定义域为![]() ,
,![]() ,所以
,所以![]() 时,
时,
函数![]() 单调递减,
单调递减,![]() 时,函数
时,函数![]() 单调递增,
单调递增,
所以![]() 是
是![]() 的极小值点而不是最大值点,即①不正确;
的极小值点而不是最大值点,即①不正确;
对于②,令![]() ,
,
则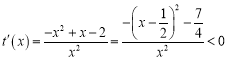 ,
,
则函数![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
,
![]() ,
,
所以函数![]() 有且只有1个零点,即②正确;
有且只有1个零点,即②正确;
对于③,![]() ,可得
,可得![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 时,函数
时,函数![]() 单调递增,
单调递增,
![]() 时,函数
时,函数![]() 单调递减,
单调递减,
则![]() ,所以
,所以![]() ,
,
即![]() 在
在![]() 上函数单调递减,且
上函数单调递减,且![]() ,
,![]() 无最小值,
无最小值,
所以不存在正实数![]() ,使得
,使得![]() 恒成立,即③不正确;
恒成立,即③不正确;
对于④,对任意两个不相等的正实数![]() ,
,
若![]() ,则
,则![]() ,④正确.
,④正确.
证明如下:
由函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
不妨设![]() ,则
,则![]() ,则
,则
![]()
![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,
,
则![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() ,所以
,所以![]() ,
,
又因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
故![]() ,即④正确.
,即④正确.
故答案为:②④


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,则下列说法中不正确的是( )
A.由样本数据得到的回归方程![]() 必过样本点的中心
必过样本点的中心![]() .
.
B.残差平方和越小的模型,拟合的效果越好.
C.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 的值越小,说明模型的拟合效果越好.
的值越小,说明模型的拟合效果越好.
D.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
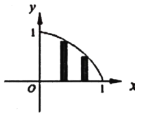
【题目】在平面直角坐标系中,函数![]() 在第一象限内的图像如图所示,试做如下操作,把
在第一象限内的图像如图所示,试做如下操作,把![]() 轴上的区间
轴上的区间![]() 等分成
等分成![]() 个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数![]() 的图像上.若用
的图像上.若用![]() ,表示第
,表示第![]() 个矩形的面积,
个矩形的面积,![]() 表示这
表示这![]() 个矩形的面积总和.
个矩形的面积总和.
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明等式:![]() ;
;
(Ⅲ)求![]() 的值,并说明
的值,并说明![]() 的几何意义.
的几何意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
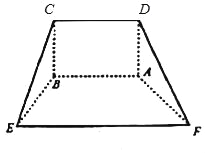
【题目】如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且![]() ,平面ABCD⊥平面ABEF
,平面ABCD⊥平面ABEF
(1)求证:BE⊥DF;
(2)求三棱锥C﹣AEF的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁餐厅新店开业打算举办一次食品交易会,招待新老顾客试吃项目经理通过查阅最近5次食品交易会参会人数x(万人)与餐厅所用原材料数量y(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) | 13 | 9 | 8 | 10 | 12 |
原材料(袋) | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出y关于x的线性回归方程![]()
(2)已知购买原材料的费用C(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
参考公式: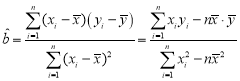 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了激励业务员的积极性,对业绩在60万到200万的业务员进行奖励奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元同时奖金不超过业绩值的5%.
(1)若某业务员的业绩为100万核定可得4万元奖金,若该公司用函数![]() (k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知
(k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知![]() ,
,![]() )
)
(2)若采用函数![]() 作为奖励函数模型试确定最小的正整数a的值.
作为奖励函数模型试确定最小的正整数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com